\(\overrightarrow{\mathrm{T}}=\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}=-\mathrm{MB} \sin \theta\)
\(\mathrm{I} \alpha=-\mathrm{MB} \sin \theta\)
for small \(\theta\)
\(\alpha=-\frac{\mathrm{MB}}{\mathrm{I}} \theta\)
\(\omega=\sqrt{\frac{\mathrm{MB}}{\mathrm{I}}}=\sqrt{\frac{(\mathrm{I})\left(\pi \mathrm{R}^{2}\right) \mathrm{B}}{\left(\frac{\mathrm{mR}^{2}}{2}\right)}}\)
\(\omega=\sqrt{\frac{2 \mathrm{I} \pi \mathrm{B}}{\mathrm{m}}}\)
\(\therefore \mathrm{T}=\frac{2 \pi}{\omega}=\sqrt{\frac{2 \pi \mathrm{m}}{\mathrm{IB}}}\)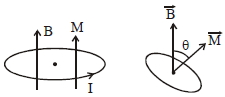
Download our appand get started for free
Similar Questions
- 1$G$ અવરોધવાળુ ગેલ્વેનોમીટરને $R _{1}$ અવરોધક શ્રેણીમાં જોડતા વૉલ્ટમીટર ની રેન્જ $0-1\, V$ ની થાય છે. $R _{1}$ સાથે વધારાનો અવરોધ ઉમેરતા વૉલ્ટમીટરની રેન્જ $0-2\, V$ ની થાય છે. તો વધારાનો અવરોધ.View Solution
- 2$M$ દળ અને $q$ વિદ્યુતભાર અચળ વેગ $V$ થી ઘન $x$ - દિશામાં ગતિ કરે છે.અચળ ચુંબકીયક્ષેત્ર $B$, $x = a$ થી $x =b$ ૠણ $Z$ દિશામાં વિસ્તરેલ છે.તો $V$ નું લઘુત્તમ મૂલ્ય કેટલું હશે,કે તે $ x > b $ માં માત્ર દાખલ થાય?View Solution
- 3એકમ દળ દીઠ વિદ્યુતભાર $\alpha$ ધરાવતો એક કાણ ઉદગમથી વેગ $\bar{v}=v_0 \hat{i}$ સાથે એકરૂપ ચુંબકીય ક્ષેત્ર $\bar{B}=-B_0 \hat{k}$ માં છોડવામાં આવે છે, જો કણ $(0, y, 0)$ માંથી પસાર થાય, તો $y$ બરાબરView Solution
- 4વિધાન $- 1$ : એક વિજભારિત કણ સ્થિત ચુંબકીયક્ષેત્રને લંબ ગતિ કરે છે. આ ગતિ દરિમિયાન વિજભારિત કણની ગતિઉર્જા બદલાતી નથી.View Solution
વિધાન $- 2$ : સ્થિત ચુંબકીયક્ષેત્ર ગતિ કરતાં વિજભારિત કણ પર ચુંબકીયક્ષેત્રને લંબ દિશામાં બળ લગાવે છે.
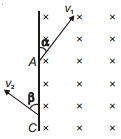
- 5$m$ દળનો અને $-q$ વિદ્યુતભાર ધરાવતો એક કણ એકરૂપ ચુંબકીય ક્ષેત્રમાં $A$ પાસે $v_1$ ઝડપથી $\alpha$ ખૂણે દાખલ થાય છે અને $C$ પાસે $v_2$ ઝડપથી આકૃતિમાં દર્શાવ્યા પ્રમાણે $\beta$ ખૂણે બહાર આવે તોView Solution
- 6બે લાંબા પાતળા $d$ અંતરે રહેલા સમાંતર તારમાંથી સમાન દિશામાં $i$ જેટલો પ્રવાહ વહેતો હોય તો ....View Solution
- 7$2.0\,eV$ ની ગતિઊર્જા ધરાવતો પ્રોટોન $\frac{\pi}{2} \times 10^{-3}\,T$ ના સમાન ચુંબકીય ક્ષેત્રમાં ગતિ કરે છે. ચુંબકીય ક્ષેત્રની દિશા અને પ્રોટોનના વેગ વચ્ચેનો ખૂણો $60^{\circ}$ છે. પ્રોટોન દ્વારા લેવામાં આવેલા હેલિકલ પથની પિચ .......... $cm$ છે (પ્રોટોનનું દળ $=1.6 \times 10^{-27}\,kg$ અને પ્રોટોન પરનો વિદ્યુતભાર $ =1.6 \times 10^{-19}\,kg$ લો,)View Solution
- 8એક ઈલેકટ્રોન ધન$-x$ અક્ષ પર ગતિ કરે છે.જો ઋણ $z-$અક્ષની સમાંતર દિશામાં સમાન ચુંબકીય ક્ષેત્ર લગાડવામાં આવે તો,View Solution
$A$. ઈલેકટ્રોન ધન$-y$ અક્ષ પર ચુંબકીય બળ અનુભવશે.
$B$. ઈલેકટ્રોન ઋણ$-y$ અક્ષ પર ચુંબકીય બળ અનુભવશે.
$C$. ઈલેકટ્રોન કોઈ પણ પ્રકારનું બળ ચુંબકીય ક્ષેત્રમાં અનુભવતું નથી.
$D$. ઇલેકટ્રોન ધન$-x$ અક્ષ પર સતત ગતિ કરશે.
$E$. ઈલેકટ્રોન ચુંબકીય ક્ષેત્રમાં વર્તુળાકાર પથ પર ગતિ કરશે.
યોગ્ય જવાબ નીચેના વિકલ્પોમાથી પસંદ કરો:
- 9View Solutionએક વિદ્યુતભારિત કણ ચુંબકીય ક્ષેત્રને લંબ ગતિ કરે છે, તો .....
- 10કોઈ વિસ્તારમાં ચુંબકીય ક્ષેત્ર $\vec{B}=B_0\left(1+\frac{x}{l}\right) \hat{k}$ અસ્તિત્વ ધરાવે છે.$l$ બાજુની અને $i$ વિદ્યુતપ્રવાહ ધરાવતી એક ચોરસ રીંગ તેની બાજુઓ $x-y$ અક્ષને સમાંતર રહે તે રીતે.રીંગ વડે અનુભવતા કુલ ચુંબકીય બળની માત્રા શોધો.View Solution
