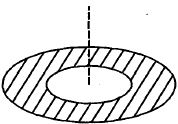
Eleatric field due to complete disc \((R=2 a)\) at a distance \(x\) and on its axis
\(E_{1}=\frac{\sigma}{2 \varepsilon_{0}}\left[1-\frac{x}{\sqrt{R^{2}+x^{2}}}\right]\)
\(E_{1}=\frac{\sigma}{2 \varepsilon_{0}}\left[1-\frac{h}{\sqrt{4 a^{2}+h^{2}}}\right]\)
\( = \frac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \frac{h}{{2a}}} \right]\)
\(\left[ \begin{gathered}
{\text{ here }}x = h{\text{ }} \hfill \\
{\text{and }},R = 2a \hfill \\
\end{gathered} \right]\)
Similarly, electric field due to disc \((R=a)\)
\(E_{2}=\frac{\sigma}{2 \varepsilon_{0}}\left(1-\frac{h}{a}\right)\)
Electric field due to given disc \(E=E_{1}-E_{2}\)
\(\frac{\sigma}{2 \varepsilon_{0}}\left[1-\frac{h}{2 a}\right]-\frac{\sigma}{2 \varepsilon_{0}}\left[1-\frac{h}{a}\right]-\frac{\sigma h}{4 \varepsilon_{0} a}\)
Hence, \(c=\frac{\sigma}{4 a \varepsilon_{0}}\)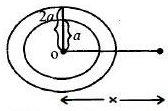
Download our appand get started for free
Similar Questions
- 1એક સમધનની કોઈ એક બાજુનાં મધ્યસ્થાન આગળ $q$ વિદ્યુતભાર મૂકવામાં આવેલ છે. સમધન સાથે સંકળાયેલ ફ્લકસ. . . . . . . . હશે.View Solution
- 2$4.9 \times 10^{5} \;N / C$ મૂલ્ય ધરાવતું શિરોલંબ વિદ્યુતક્ષેત્ર, $0.1 \,g$ દળ ધરાવતા પાણીના બુંદને નીચે પડતું આટકાવવા પૂરતું છે. બુંદ પરનો વિધુતભાર........$ \times 10^{-9} \;C$ હશેView Solution
[$g =9.8 \,m / s ^{2}$ આપેલા ]
- 3બે સમાન ત્રિજ્યાના સૂક્ષ્મ વાહક ગોળા પરનો વિદ્યુતભાર $10\ \mu C$ અને $- 20\ \mu C$ છે. જે તેમની વચ્ચે અનુભવાતા બળ $F_1$ થી $R$ અંતરે મૂકેલા છે. જો તેઓ એકબીજાના સંપર્કમાં હોય અને પછી સમાન અંતરે અલગ કરવામાં આવે તો તેઓ વચ્ચે અનુભવાતું બળ $F_2$ છે. તો $F_1$ થી $F_2$ ગુણોત્તર શોધો.View Solution
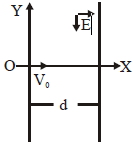
- 4એક વિજભારિત કણ ($m$ દળ અને $q$ વિજભાર) $X$ અક્ષ દિશામાં $V _{0}$ વેગથી ગતિ કરે છે.જ્યારે તે ઉગમબિંદુ પાસેથી પસાર થાય ત્યારે તે $\overrightarrow{ E }=- E \hat{ j }$ જેટલા એકસમાન વિદ્યુતક્ષેત્રમાં (જે $x = d$ સુધી પ્રવર્તે છે) દાખલ થાય છે. $x > d$ ક્ષેત્રમાં ઇલેક્ટ્રોનના ગતિપથનું સમીકરણ શું હશે?View Solution
- 5$+3\,Q$ વિદ્યુતભાર ધરાવતા ગોળાને $-Q$ વિદ્યુતભાર ધરાવતી ગાળીય કવચની અંદર સમકેન્દ્રિય મૂકેલ છે.ગોળાની ત્રિજયા $a$ એ ગોળીય કવચની ત્રિજયા $b(b>a)$ કરતાં નાની છે.હવે,કેન્દ્રથી $R>a$ બિંદુએ વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 6$a$ બાજુવાળા ચોરસના કેન્દ્રની ઉપર $a/2$ અંતરે $q$ વિદ્યુતભાર મૂકતાં સમઘનની કોઇ એકબાજુમાંથી કેટલુ ફલ્કસ પસાર થાય?View Solution
- 7સમાન મૂલ્ય q ધરાવતા બે વિદ્યુતભારો $X-$ અક્ષ પર $ x=-a$ અને $x=a$ આગળ રાખેલ છે. $m$ દળ ધરાવતો અને $q_0=\frac{q}{2}$ વિદ્યુતભાર ધરાવતો એક કણ ઊગમબિંદુ પર મૂકેલ છે.હવે જો $q_0$ વિદ્યુતભારને $Y-$ અક્ષની દિશામાં શૂક્ષ્મ સ્થાનાંતર $(y < < a) $ આપવામાં આવે,તો કણ પર લાગતું પરિણામી બળ _______ ના સમપ્રમાણમાં હશે.View Solution
- 8$q_1$ બિંદુવત વિદ્યુતભાર $q_2$ વિદ્યુતભાર પર $F$ બળ લાગુ પાડે છે. જો બીજો એક વિદ્યુતભાર $q_3$ ને $q_2$ વિદ્યુતભારની એકદમ નજીક મૂકવામાં આવે તો $q_1$ વિદ્યુતભાર દ્વારા $q_2$ વિદ્યુતભાર પર લાગતું બળ કેટલું હશે ?View Solution
- 9$1$ કુલંબનો વિદ્યુતભાર $10 \,cm$ ત્રિજ્યાના ગોળાના અને $20 \,cm$ બાજુના સમઘનના કેન્દ્ર પાસે રહેલો છે. ગોળા અને સમઘનમાંથી બહાર જતા ફલક્સનો ગુણોત્તરView Solution
- 10$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.?View Solution
