$A$ તથા $B$ વચ્ચેની પ્રક્રિયામાં $A$ ના સંદર્ભમાં પ્રક્રિયાક્રમ $2$ છે. તથા $B$ ના સંદર્ભમાં પ્રક્રિયાક્રમ $3$ છે. જો $A$ તથા $B$ બંનેની સાંદ્રતા બમણી કરવામાં આવે તો પ્રક્રિયાક્રમ .............. ના ગુણકથી વધશે.
NEET 2013, Medium
Download our app for free and get started
c
Formula: $a A+b B \rightarrow c C+d D$
Formula: $a A+b B \rightarrow c C+d D$
${\text {Rate}=\frac{d R}{d T}}$
${=\alpha[A]^{x} \cdot[B]^{y}}$
${=k[A]^{x} \cdot[B]^{y}}$
$\mathrm{K}=$ rate constant
Rate, $r_{1}=k[A]^{2}[B]^{3}$
On doubling the concentration, we have
$r_{2}=k[2 A]^{2}[2 B]^{3}$
$=32 k[A]^{2}[B]^{3}=32 r_{1}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેની પ્રક્રિયા માટે વેગનિયમ $k\left[ A \right]\left[ B \right]$ રજૂઆત દ્વારા આપવામાં આવે છે.$A + B \to$ Product $A$ નું મૂલ્ય $0.1$ મોલ અચળ રાખીને $B$ નું મૂલ્ય $0.1$ મોલથી વધારી $0.3$ મોલ કરવામાં આવે તો વેગ અચળાંક શું થશે ?View Solution
- 2પ્રથમક્રમની એક પ્રક્રિયામાં $2 × 10^4$ સેકન્ડમાં પ્રક્રિયાની સાંદ્રતા $800$ મોલ/ડેસીમી $^3$ થી ઘટીને $50$ મોલ/ડેસીમી $^3$ થાય છે. તો પ્રક્રિયાનો વેગ-અચળાંક કેટલો થશે ?View Solution
- 3ઉષ્માક્ષેપક પ્રક્રિયા માટે જ્યારે પ્રક્રિયાની એન્થાલ્પી $\Delta$$H$ $ KJ/$ મોલમાં છે. તો સક્રિયકરણ ઊર્જા માટેનું ન્યનતમ મૂલ્ય ......થશે.View Solution
- 4પ્રથમ ક્રમની પ્રક્રિયાનો વિશિષ્ટ પ્રક્રિયાવેગ $10^{-2}\, sec^{-1}$ છે. તો પ્રક્રિયકના $20\, g$ ઘટીને $5\, g$ થવા માટે ........ $\sec$ લાગશે.View Solution
- 5જ્યારે તાપમાન $40^{\circ} C$ થી $30^{\circ} C$માં બદલાયું ત્યારે પ્રક્રિયા વેગમાં $3.555$ ગણો ઘટાડો થયો.ત્યારે પ્રક્રિયાની સક્રિયકરણ ઊર્જા ...............$kJ\, mol ^{-1}$ છેView Solution
[લો; $R =8.314 \,J\, mol ^{-1}\, K ^{-1}$ In $3.555=1.268$]
- 6જો ${t_{\frac{1}{4}}}$ એ પ્રક્રિયકની સાંદ્રતા મૂળ સાંદ્રતા ઘટીને $\frac{3}{4}$ જેટલી થવા લાગતો સમય હોય અને પ્રથમ ક્રમની પ્રક્રિયાનો વેગ અચળાંક $K$ હોય, તો ${t_{\frac{1}{4}}}$ ........ થાય.View Solution
- 7જો પ્રક્રિયા વેગ $ = K$ $ C_A$$^{3/2}$$C_B$$^{-1/2}$ હોય તો પ્રક્રિયા ક્રમ જણાવો.View Solution
- 8View Solutionદ્વિતીય ક્રમની પ્રક્રિયા માટે વેગઅચળાંકનો એકમ .... થશે.
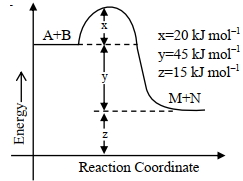
- 9નીચેના આંકડા મુજબ, પ્રક્રિયાના એન્થાલ્પી ફેરફારની તીવ્રતાView Solution
${A}+{B} \rightarrow {M}+{N}$ $......$ ${kJ} {mol}^{-1}$ બરાબર છે. (નજીકના પૂર્ણાંકમાં)
- 10પ્રક્રિયા $2{N_2}{O_5} \to 4N{O_2}$ $ + {O_2}$ નો વેગ અચળાંક $3 \times {10^{ - 5}}{\sec ^{ - 1}}$ છે. જો પ્રક્રિયાનો વેગ $2.40 \times {10^{ - 5}}\,mol\,\,litr{e^{{\rm{ - 1}}}}{\sec ^{ - 1}}$ હોય, તો ${N_2}{O_5}$ ની સાંદ્રતા ( $mol\,L^{-1}$ માં ) .............. થશે.View Solution