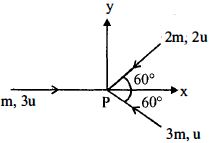
From the law of consevation of momentum we know that,
\(\begin{array}{l}
{m_1}{u_1} + {m_2}{u_2} + ...... = {m_1}{v_1} + {m_2}{v_2} + ....\\
Given\,{m_1}\, = \,m,{m_2} = 2m\,and\,{m_3} = 3m\\
and\,{u_1} = 3u,\,{u_2} = 2u\,and\,{u_3} = u
\end{array}\)
Let the velocity when the stick \(= \overrightarrow v \)
Then, according to question,
\(\begin{array}{l}
m \times 3u\left( i \right) + 2m \times 2u\left( { - \hat i\cos {{60}^ \circ } - \hat j\sin {{60}^ \circ }} \right)\\
+ 3\,m \times u\left( { - \hat i\cos {{60}^ \circ } + \hat j\sin {{60}^ \circ }} \right)\\
= \left( {m + 2m + 3m} \right)\,\overrightarrow v \\
\Rightarrow \,3mu\hat i - 4mu\frac{{\hat i}}{2} - 4mu\left( {\frac{{\sqrt 3 }}{2}\hat j} \right) - 3mu\frac{{\hat i}}{2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 3mu\left( {\frac{{\sqrt 3 }}{2}\hat j} \right) = 6m\,\overrightarrow v \\
\Rightarrow \,mu\hat i\, - \frac{3}{2}mu\hat i - \frac{{\sqrt 3 }}{2}mu\hat j = 6m\,\overrightarrow v \\
\Rightarrow \frac{1}{2}mu\hat i - \frac{{\sqrt 3 }}{2}mu\hat j = 6m\,\overrightarrow v \\
\Rightarrow \,\overrightarrow v = \frac{u}{{12}}\,\left( { - \hat i - \sqrt 3 \hat j} \right)
\end{array}\)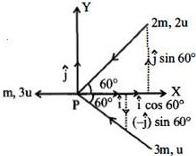
Download our appand get started for free
Similar Questions
- 1$40 kg$ ના પદાર્થનો વેગ $ 4 m/s$ છે.અને $60 kg$ ના પદાર્થનો વેગ $ 2 m/s $ છે.બંને વચ્ચે અસ્થિતિસ્થાપક સંધાત થાય,તો ગતિઊર્જામાં કેટલા ......... $J$ ઘટાડો થશે?View Solution
- 2એક પવન સંચાલિત જનરેટર પવન ઉર્જા ને વિદ્યુતઉર્જામાં રુપાંતરીત કરે છે.ધારો કે જનરેટર તેના પાંખિયા દ્વારા પવનઉર્જાના ઘર્ષણ ને વિદ્યુત ઉર્જા માં રુપાંતરીત કરે છે.પવનની ઝડપ $v$ માટે, મેળવેલ વિદ્યુત પાવર કઈ રીતે સમપ્રમાણ માં હશે?View Solution
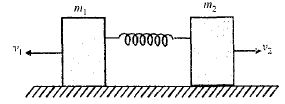
- 3કોઈ સ્પ્રિંગ ને સમક્ષિતિજ ઘર્ષણ રહિત સપાટી પર આકૃતિમાં બતાવ્યા પ્રમાણે બે $m_1$ અને $m_2$ દળ ધરાવતા બે બ્લોક ની વચ્ચે સંકોચન કરવવામાં આવે છે. જ્યારે બ્લોક ને મુક્ત કરવામાં આવે છે, ત્યારે તેનો પ્રારંભિક વેગ $v_1$ and $v_2$ છે. સ્થિર થયા પહેલા બ્લોક દ્વારા કાપેલ અંતર અનુક્રમે $x_1$ અને $x_2$ હોય તો $\left( {\frac{{{x_1}}}{{{x_2}}}} \right)$ નો ગુણોત્તર શું થાય?View Solution
- 4View Solutionસ્થિર સ્થિતિમાં રહેલા પદાર્થ પાસે શું હશે ?
- 5$2000 kg$ દળની એક ગાડી $1$ મિનિટમાં $30m$ અંતર સુધી એક ક્રેન દ્વારા ઉંચકવામાં આવી છે. બીજી ક્રેન આ જ ક્રિયા $2$ મિનિટમાં કરે છે. દરેક ક્રેઈનને આપવામાં આવતો પાવર અનુકમે ..... હશે.View Solution
- 6$m$ દળનાં એક કણને $u$ ઝડપે જમીનના સમક્ષિતિજ સાથે $\theta$ કોણે પ્રક્ષેપિત કરવામાં આવે છે. તેની ઊર્ધ્વગતિ દિશામાં ગતિ દરમિયાન ગુરુત્વાકર્ષણ વડે થયેલ કાર્ય કેટલું હશે?View Solution
- 7$\left(3 x^2+2 x-5\right) \mathrm{N}$ જેટલું બળ વસ્તુને $x=2 \mathrm{~m}$ થી $x=4 \mathrm{~m}$ આગળ ખસેડે છે. બળ દ્વારા થતું કાર્ય ............ $J$ હશે.View Solution
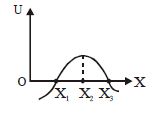
- 8આકૃતિમાં બતાવ્યા અનુસાર, અહી એક કણની સ્થિતિઉર્જા $U$ નો તેના ઉગમબિંદુથી સ્થાન $x$ વિદુદ્ધનો આલેખ દર્શાવેલ છે. નીચેનામાંથી ક્યુ વિધાન સાયું છે. કણ એView Solution
- 9$5 : 3 $ વજનનો ગુણોત્તર ઘરાવતા બે માણસ પગથીયા ચડવાના સમયનો ગુણોત્તર $ 11 : 9$ હોય,તો પાવરનો ગુણોત્તર શોધો.View Solution
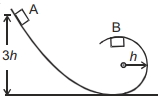
- 10આકૃતિ માં દર્શાવ્યા મુજબ, એક પદાર્થને લીસા ટ્રેક ઉપર $A$ સ્થાને થી છોડવામાં આવે છે. જ્યારે પદાર્થ $B$ પર પહોંચે છે, ત્યારે ટ્રેક વડે તેના પર લાગેલ લંબપ્રતિક્રિયા બળ ....... છે?View Solution