આકૃતિમાં આપેલા આલેખમાં પ્રક્ષિપ્ત ગતિ સાથે સંકળાયેલી રાશિ કઈ છે જે $y$-અક્ષ પર દોરવામાં આવી છે ?
Easy
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પદાર્થ ઉદગમબિદુથી શરૂ કરે છે જેનો પ્રવેગ $6 m/s^2$ $x$ દિશામાં અને $8 m/s^2$ $y$ દિશામાં, તો તેણે $4\,sec$ માં ........ $m$ અંતર કાપશે.View Solution
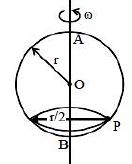
- 2એક $2\pi r$ લંબાઈના તારને વાળીને એક વર્તુળ બનાવીને શિરોલંબ સમતલમાં મૂકવામાં આવે છે એક મણકો તાર પર સરળતાથી સરકી શકે છે જ્યારે વર્તુળને આકૃતિમાં દર્શાવ્યા મુજબ $AB$ની સાપેક્ષે $\omega$ જેટલી કોણીય ઝડપથી ફેરવતા મણકો વર્તુળની સાપેક્ષે $P$ બિંદુ પાસે સ્થિર થાય છે તો $\omega^2$ નું મૂલ્ય કેટલું હશે?View Solution
- 3એક માણસ મહત્તમ $136\,m$ શિરોલંબ ઊંચાઈ સુધી બોલ ફેકી શકે છે. સમાન બોલને મહત્તમ સમક્ષિતિજ કેટલા અંતર ($m$ માં) સુધી ફેંકી શકે છે તે $.....\,m$ છેView Solution
- 4જો સદિશ $\overrightarrow {A} = cos\omega t\hat i + sin\omega t\hat j$ અને$\overrightarrow {B} = cos\frac{{\omega t}}{2}\hat i + sin\frac{{\omega t}}{2}\hat j$ સમયના વિધેયો હોય, તો કયા $t$ સમયે આ બંને સદિશો પરસ્પર લંબ થશે?View Solution
- 5અચળ ઝડપે એક કણ વર્તુળાકાર માર્ગ ફરે છે. જયારે કણ $90^{\circ}$ નો ખૂણો બનાવે છે, ત્યારે તેનો તત્કાલીન વેગ અને સરેરાશ વેગનો ગુણોતર $\pi: x \sqrt{2}$ છે. $x$ ની કિમત ....... હશે.View Solution
- 6પ્રક્ષિપ્ત પદાર્થને એક પ્રક્ષેપને ક્ષિતિજ સાથે $30^{\circ}$ પર અને $40\,ms ^{-1}$ ના શરૂઆતી વેગ સાથે પ્રક્ષેપિત કરવામાં આવેલ છે. શરૂઆતથી $t=2\,s$ માટે પ્રક્ષેપનો વેગ ........ હશે. $\left( g =10 m / s ^2\right)$View Solution
- 7એક કણ $t =0$ સમયે બિંદુ $\left( {2.0\hat i + 4.0\hat j} \right)\,m$ થી પ્રારંભિક $\left( {5.0\hat i + 4.0\hat j} \right)\,m{s^{ - 1 }}$ ના વેગથી ગતિ કરે છે. તેની ઉપર અચળ બળ લગાડતા તે અચળ પ્રવેગ $\left( {4.0\hat i + 4.0\hat j} \right)\,m{s^{ - 2}}$ ઉત્પન્ન કરે છે. $2s$ પછી ઉગમ બિંદુથી કણનું અંતર કેટલું હશે?View Solution
- 8એક પૈડું $3000 \,rpm$ ની કોણીય ઝડપથી ભ્રમણ કરે છે. તો $1 \,sec$ માં તે કેટલું કોણીય સ્થાનાંતર કરશે?View Solution
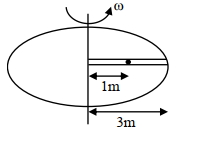
- 9એક વર્તુળાકા ટેબલ $\omega$ રેડિયન/સેકંડના કોણીય વેગથી તેની અક્ષને ફરતે ભ્રમણ કરે છે. ટેબલની ત્રિજ્યાવર્તી દિશામાં એક લીસો ખાંચો રહેલો છે. એક સ્ટીલના ગોળાને $1 \mathrm{~m}$ ના અંતરે ખાંચામાં હળવેકથી મૂકવામાં આવે છે. જો ટેબલની ત્રિજ્યા $3 \mathrm{~m}$ હોય, તો ગોળાનો ટેબલની સાપેક્ષ જે સમયે ગોળો ટેબલમાંથી છૂટે તેની સાપેક્ષ ત્રિજ્યાવર્તી વેગ $x \sqrt{2} \omega \mathrm{m} / \mathrm{s}$ છે, જ્યાં $x$ નું મૂલ્ય. . . . . . છે.View Solution
- 10View Solutionએક પદાર્થ વર્તુળાકાર પથ પર નિયમિત વર્તુળમય ગતિ કરે છે.તો તેનો