આકૃતિમાં બે થમોડાયનેમિક પ્રક્રિયાઓ દર્શાવેલ છે. પ્રકિયા $\mathrm{A}$ અને $\mathrm{B}$ માટે મોલર ઉષ્મા ધારિતા $\mathrm{C}_{\mathrm{A}}$ અને $\mathrm{C}_{\mathrm{B}}$ છે. અચળ દબાણે અને અચળ કદે મોલર ઉષ્મા ધારિતા અનુકમે $\mathrm{C}_{\mathrm{P}}$ અને $\mathrm{C}_{\mathrm{V}}$ છે. સાચું વિધાન પસંદ કરો.
JEE MAIN 2024, Diffcult
Download our app for free and get started
c
For process \(\mathrm{A}\)
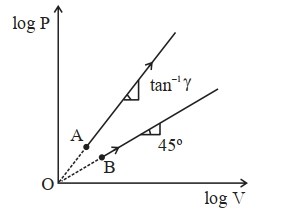
For process \(\mathrm{A}\)
\( \log P=\gamma \log \mathrm{V} \Rightarrow \mathrm{P}=\mathrm{V}^\gamma,(\gamma>1) \)
\( P V^{-\gamma}=\text { Constant } \)
\( C_A=C_V+\frac{R}{1+\gamma} \ldots . \text { (i) }\)
Likewise for process \(\mathrm{B} \rightarrow P V^{-1}=\) \(Cons\) \(\tan t\)
\(C_B\) \( =C_v+\frac{R}{1+1} \)
\(C_B\) \( =C_v+\frac{R}{2} \) \(.............(ii)\)
\(C_P\) \(=C_v+R\) \(...........(iii)\)
By \((i)\), \((ii)\) & \((iii)\) \(C_P>C_B>C_A>C_v\) [No answer matching]
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2$ મોલ હિલિયમ વાયુનું તાપમાન $0°C$ થી $100°C$ વધારવા અચળ કદે અને અચળ દબાણે અનુક્રમે ......ઉષ્મા જરૂરી છે.View Solution
- 2એક પાત્રમાં $7\, g$ નાઈટ્રોજન અને $11\, g$ કાર્બન ડાયોક્સાઈડનું મિશ્રણ $T= 290 K$ તાપમાને છે. જો મિશ્રણનું દબાણ $1 atm (1.01 \times 10^5 ,N/m^{2})$ છે તો ઘનતાનું મૂલ્ય..... $kg/m^3$ થાય.View Solution
- 3એક નળાકારમાં વાયુ ભરેલો છે, તેનું તાપમાન $20\%$ વધારતા $ (k)$ તેનું કદ $10\%$ ઘટે છે. કેટલા $\%$ વાયુ બહાર વ્યય થયો હશે ?View Solution
- 4બે દ્વિ પરમાણ્વિક વાયુ $\mathrm{A}$ અને $\mathrm{B}$ $T$ તાપમાને છે. વાયુ $A$ ના અણુંનું દળ $m$ અને તે દઢ છે જ્યારે વાયુ $\mathrm{B}$ ના અણુનું દળ $\frac{\mathrm{m}}{4}$ અને તેમાં વધારાની કંપન ગતિ છે. $\mathrm{A}$ અને $\mathrm{B}$ વાયુની વિશિષ્ટ ઉષ્મા $(\mathrm{C}_{\mathrm{v}}^{\mathrm{A}}$ અને $\mathrm{C}_{\mathrm{v}}^{\mathrm{B}})$ નો ગુણોત્તર કેટલો થાય?View Solution
- 5જો તાપમાન $27°C$ થી $927°C$ વધારવામાં આવે તો વાયુની ગતિ ઊર્જા કેટલી થાય ?View Solution
- 6એક પરમાણ્વિક આદર્શ વાયુનાં ચોક્કસ જથ્થાનું અચળ દબાણે તેનું તાપમાન $10^{\circ} C$ જેટલું વધારવા માટે $20 \,J$ ઉષ્મા ઊર્જાની જરૂર પડે છે. તો અચળ કદે એટલું જ તાપમાન વધારવામાં ........... $J$ ઉષ્માની જરૂર પડે.View Solution
- 7બે આદર્શ પદાર્થ એક એવા દ્રવ્યમાંથી બનેલો છે, કે જેની ઉષ્માધારિતા તાપમાન સાથે વધતી જાય છે. જો આમાંથી એક પદાર્થનું તાપમાન $100^oC$ અને જ્યારે બીજા પદાર્થનું તાપમાન $0^oC$ છે. જો આ બંનેને એકબીજાનના સંપર્કમાં રાખીએ અને આ પ્રક્રિયામાં ઉષ્માનો વ્યય થતો ન હોય, તો બંને પદાર્થોનું અંતિમ તાપમાન કેટલું હશે?View Solution
- 8View Solutionવાયુ દ્ઢ દ્વિ પરમાણ્વિક અણુ ધરાવે છે જે શરૂઆતમાં સામાન્ય પરિસ્થિતિમાં છે. વાયુને સમોષ્મિ સંકોચન કરીને કદ પાંચમા ભાગનું કરતાં અણુની અંતિમ પરિસ્થિતિમાં ભ્રમણ કરતાં અણુની સરેરાશ ગતિઊર્જા કેટલી હશે?
- 9ચોક્કસ દળના વાયુનું અચળ દબાણે તાપમાન $50^{\circ} C$ જેટલું વધારવા માટે $160$ કેલરી ઉર્જાની જરૂર પડે. જ્યારે સમાન દળના વાયુને અચળ કદે $100^{\circ} C$ જેટલો ઠંડો પડતાં તે $240$ કેલરી ઉષ્મા મુક્ત કરે છે. આ વાયુના અણુના મુક્તતાના કેટલા હશે? (વાયુને આદર્શ વાયુ ગણો)View Solution
- 10મુક્તતા અંશો માટે ક્યું વિદ્યાન સાયું છે ?View Solution
$(A)$ $n$ મુક્તતાનાં અંશો ધરાવતા એક અણુ પાસે $n ^2$ જેટલા ઊર્જા સંગ્રહ કરવાના જુદા-જુદા રસ્તાઓ હશે.
$(B)$ દરેક મુક્તતા અંશ એ પ્રતિ મોલ સરેરાશ ઊર્જાના $\frac{1}{2}RT$ સાથે સંકળાયેલા હશે.
$(C)$ એક પરમાણ્વીય વાયુ અણુ પાસે એક ભ્રમણ ગતિકીય મુક્તતા અંશ જ્યારે દ્વિપરમાણ્વીય પાસે બે ભ્રમણાગતિકીય મુક્તતા અંશો હશે.
$(D)$ $CH _4$ પાસે કુલ $6$ મુક્તતા અંશો હશે.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.