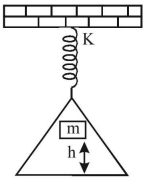
આકૃતિમાં બતાવ્યા પ્રમાણે $h$ ઊંચાઈ પર $m$ દળનો ભાર તવા પર પરે છે જે સ્પ્રિગથી લટકાવેલ છે. જો સ્પ્રિગ અચળાંક $k$ હોય અને તવાનું દળ શૂન્ય હોય અને દળ $m$ એ તવાની સાપેક્ષમાં ઉછળે નહી, તો કંપનનો કંપનવિસ્તાર $............$

Diffcult
b
(b)
(b)
According to energy conservation principle,
If, \(x _1\) is maximum elongation in the spring when the particle is in its lowest extreme position. Then,
\(mgh =\frac{1}{2} kx _1^2- mgx _1\)
\(\Rightarrow \frac{1}{2} kx _1^2- mgx _1- mgh =0\)
\(\text { or, } x _1^2-\frac{2 mg }{ k } x _1-\frac{2 mg }{ k } \cdot h =0\)
\(\therefore x _1=\frac{2 mg }{ k } \pm \sqrt{\left[\left(\frac{2 mg }{ k }\right)^2+4 \times \frac{2 mg }{ k } h \right]}\)
Amplitude \(A= x _1 -x _0\) (elongation in spring for equilibrium position)
\(A =\frac{ mg }{ k } \sqrt{\left(1+\frac{2 hk }{ mg }\right)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્પિંગથી લટકાવેલ $m$ દળની કંપનની આવૃતિ $v_1$ છે. સ્પ્રિંગની લંબાઈ તેની મૂળ લંબાઈના ત્રીજા ભાગની કરવામાં આવે ત્યારે તે $m$ દળની આવૃત્તિ $v_2$ છે. આથી,View Solution
- 2$200\; gm$ ના દળને $80 \;N/m$. બળઅચળાંક ઘરાવતી સ્પ્રિંગ પર લટકાવેલ છે તેનો આવર્તકાળ કેટલો ..... $\sec$ થાય?View Solution
- 3બળપ્રેરિત દોલનોમાં કણનો કંપવિસ્તાર બળની $\omega_{1}$ આવૃતિ માટે મહત્તમ, જ્યારે બળની $\omega_{2}$ આવૃતિ માટે ઉર્જા મહત્તમ હોય, તોView Solution
- 4$A$ સૂક્ષ્મ કંપવિસ્તાર અને $T$ આવર્તકાળ ધરાવતા સાદા લોલકના ગોળાની એક આવર્તકાળમાં સરેરાશ ઝડપ કેટલી હશે?View Solution
- 5એક રિંગને ખીલી પર લટકાવેલ છે, તે સરક્યાં અને ગબડ્યા વગર આવર્તગતિ કરે છે. $(i)$ તેના સમતલમાં તેનો આવર્તકાળ $T_{1}$ અને, $(ii)$ આગળ અને પાછળ સમતલને લેમ્બ દિશામાં તેનો આવર્તકાળ $T _{2}$ હોય તો $\frac{ T _{1}}{ T _{2}}$ નો ગુણોત્તર કેટલો થાય?View Solution
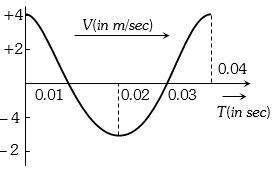
- 6સરળ આવર્તગતિ માટે વેગ વિરુઘ્ઘ સમયનો આલેખ આપેલ છે.તો આવૃત્તિ કેટલી ..... $Hz$ થાય?View Solution
- 7$100\, {Nm}^{-1}$ બળ આચાળાંક ધરાવતી સ્પ્રિંગના છેડે $1\, {kg}$ દળનો પદાર્થ લટકાવેલ છે. દળને થોડોક નીચે ખેંચીને મુક્ત કરતાં તે $T$ આવર્તકાળથી સરળ આવર્તગતિ કરે છે. જ્યારે તેની ગતિઉર્જા અને સ્થિતિઊર્જા સમાન થાય તે સમય $\frac{{T}}{{x}}$ હોય,તો ${x}$ નું મૂલ્ય કેટલું હશે?View Solution
- 8અવગણ્ય દળ ધરાવતી સ્પ્રિંગથી લટકાવેલ $M$ દળનો આવર્તકાળ $T$ છે. હવે તેની સાથે બીજુ $M$ દળ લટકાવતા હવે, દોલનનો આવર્તકાળ કેટલો થાય?View Solution
- 9$LCR$ પરિપથ અવમંદિત આવર્ત દોલનો તરીકે વર્તે છે. તેને એક $\mathrm{b}$ અવમંદન અચળાંક ધરાવતી અવમંદિત આવર્ત ગતિ કરતી સ્પ્રિંગની સાથે સરખાવતા તેના સમતુલ્ય શું થાય?View Solution
- 10પદાર્થ સરળ આવર્ત ગતિ કરે છે. સ્થિતિઉર્જા $(P.E.)$, ગતિઉર્જા $(K.E.)$ અને કુલઉર્જા $(T.E.)$ સ્થાનતર $x$ ના વિધેય સ્વરૂપે માપવામાં આવે છે. નીચેનામાંથી કયું વિધાન સાચું છે?View Solution
