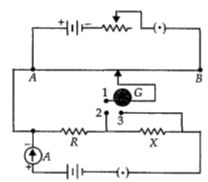
When the two way key is switched off, then The current flowing in the resistors \(R\) and \(X\) is
\(I=1 \,\mathrm{A}\) .......\((i)\)
When the key between the terminals \(1\) and \(2\) is plugged in, then
Potential difference across \(R=I R=k l_{1}\) ......\((ii)\)
where \(k\) is the potential gradient across the potentiometer wire
When the key between the terminals \(1\) and \(3\) is plugged in, then
Potential difference across \((R+X)=I(R+X)=k l_{2}\) ....\((iii)\)
From equation \((ii),\) we get
\(R=\frac{k l_{1}}{I}=\frac{k l_{1}}{1}=k l_{1} \Omega\) .......\((iv)\)
From equation \((iii),\) we get
\(R + X = \frac{{k{l_2}}}{I} = \frac{{k{l_2}}}{1} = k{l_2}\,\Omega \quad {\rm{ (Using }}({\rm{i}}))\)
\(X = k{l_2} - R\)
\( = k{l_2} - k{l_1}{\rm{ }}\,\,\,\,\,\,\,\,\,\,\,{\rm{(Using}}\left( {iv} \right){\rm{)}}\)
\(=k\left(l_{2}-l_{1}\right) \,\Omega\)
Download our appand get started for free
Similar Questions
- 1$60\,W, 230V$ નો લેમ્પ $8$ કલાક વાપરવામાં આવે છે.$1$ યુનિટના ભાવ $1.25$ રૂપિયા હોય તો $30$ દિવસમાં કેટલા રૂપિયા બીલ આવશે?View Solution
- 2જુદાં જુદાં દ્રવ્યમાંથી બનાવેલ અવરોધના $0\,^\circ$$C$ તાપમાને મૂલ્ય $R_1$ અને $R_2$ છે.તેમના અવરોધના તાપમાન ગુણાંક $\alpha $ અને $ - \beta $ છે.જો શ્રેણીમાં જોડવાથી તાપમાન સાથે સમતુલ્ય અવરોધ બદલાતો ન હોય,તો ${R_1}/{R_2}=$View Solution
- 3$2 \,volt \, emf$ અને $ 5\,\Omega$ અવરોધ ધરાવતા કોષને $100 \,cm$ લંબાઇ અને $ 15 \,\Omega$ અવરોધ ધરાવતા તાર સાથે જોડવામાં આવતાં વિદ્યુતસ્થિતિમાન પ્રચલન કેટલું થાય?View Solution
- 4$1\, mm$ અને $2\, mm$ જાડાઈના વાયરમાં સમાન કોપરનું દળ છે. બે વાયરોને શ્રેણીમાં જોડીને તેમાંથી પ્રવાહ પસાર કરવામાં આવે છે. તો વાયરમાં ઉત્પન્ન થતા પાવરનો ગુણોત્તર .... હશે.View Solution
- 5$E_1$ અને $E_2$ $emf$ના બે કોષો $\left(E_1 > E_2\right)$ ને સ્વતંત્ર રીતે પોટેન્શીયમીટર સાથે જોંડામાં આવે છે. અને તેમને અનુરૂપ બેલેન્સીંગ લંબાઈ $625\,cm$ અને $500\,cm$ હોય,તો $\frac{E_1}{E_2}$ ગુણોતર કેટલો છે.View Solution
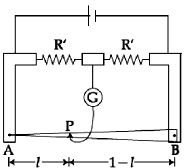
- 6એક મીટરબ્રીજમાં, $1\,m$ લંબાઈનો તાર અસમાન આડછેદ એવી રીતે ધરાવે છે કે તેના અવરોધ $R$ નો લંબાઈ $l$ સાથેનો ફેરફાર $\frac{{dR}}{{d\ell }} \propto \frac{1}{{\sqrt \ell }}$ છે. આકૃતિમાં બતાવ્યા પ્રમાણે બે સમાન અવરોધો જોડેલ છે. જ્યારે જોકી એ બિંદુ $P$ પર હોય ત્યારે ગેલ્વેનોમીટરમાં આવર્તન શૂન્ય છે. લંબાઈ $AP$ કેટલા .................. $m$ હશે?View Solution
- 7View Solutionવાહક એ અતિસુવાહક તરીકે ક્યારે વર્તે છે.
- 8બે સમાન હિટરના ફિલામેન્ટ, પ્રથમ સમાંતર અને ત્યાર બાદ શ્રેણીમાં જોડવામાં આવે છે.લગાવેલ સમાન વોલ્ટેજ માટે, સમાન સમયમાં, સમાંતર અને શ્રેણી જોડાણોમાં ઉત્પન્ન ઊર્જાનો ગુણોત્તર $.........$ થશે.View Solution
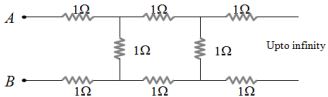
- 9આપેલ અનંત અવરોધ ધરાવતા પરીપથ માટે $A$ અને $B$ વચ્ચેનો અસરકારક અવરોધ કેટલો હશે ?View Solution
- 10View Solutionહીટરમાં વપરાતા ગૂચાળાને બે સમાન ભાગમાં વિભાજિત કરવામાં આવે છે. હવે આમાંથી એક જ ભાગનો ઉપયોગ હીટરમાં થાય છે તો તેમાંથી ઉત્પન્ન થતી ઉષ્મા પહેલા કરતાં કેવી થાય?
