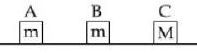
આકૃતિમાં બતાવ્યા પ્રમાણે ત્રણ ચોસલા $A, B$ અને $C$ ને લીસી સમક્ષિતિજ સપાટી પર મુકવામાં આવેલા છે. $A$ અને $B$ નું એકસરખુ દળ $m$ છે જ્યારે $C$ નું દળ $M$ છે. ચોસલા $A$ ને ચોસલા $B$ તરફ પ્રારંભિક ઝડપ $v$, આપવામાં આવે છે જેને લીધે એ ચોસલા $B$ જોડે સંપૂર્ણ અસ્થિતિસ્થાપક અથડામણ અનુભવે છે. આ સંયુક્ત દળ પણ ચોસલા $C$ સાથે સંપૂર્ણ અસ્થિતિસ્થાપક અથડામણ અનુભવે છે. અને આ આખી ઘટનામાં પ્રારંભિક ગતિ ઊર્જા $\frac{5}{6}$ ભાગ જેટલી ઊર્જાનો વ્યય થાય છે.તો $M/m $ નું મૂલ્ય શું હશે?
JEE MAIN 2019, Diffcult
Download our app for free and get started
c
Apply \(LMC\) (Linear Momentum Conservation)
Apply \(LMC\) (Linear Momentum Conservation)
\(mv = (2m + M) v'\)
\(v' = \frac{{mv}}{{2m + M}}\)
Initial energy
\(\frac{1}{2}\) \(m{v^2}\)
Final energy
\(\frac{1}{2}\,\left( {2m + M} \right){\left( {\frac{{mv}}{{2m + M}}} \right)^2}\)
\(Initial\, kinetic\, energy - Final\, Kinetic\, energy =\) \(\frac{5}{6}\) of initial kinetic energy.
After solving, we get, \(\frac{M}{m} = 4.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2\,kg$ ના નાના પદાર્થ પર $ F = 7 - 2x + 3{x^2}\,newton $ જેટલું બળ લાગતા તેમનું સ્થાનાંતર $ x = 0 $ થી $ x = 5\,m $ જેટલું થાય છે. જુલમાં થતું કાર્ય કેટલું હશે?View Solution
- 2$l$ લંબાઇની દોરી પર પદાર્થ લટકાવેલ છે,પદાર્થના નીચેના બિંદુએ કેટલો મહત્તમ વેગ આપવાથી મહત્તમ ઊંચાઇએ તણાવ શૂન્ય થાય ?View Solution
- 3$1 N$ વજન ધરાવતા પદાર્થની જમીનની સાપેક્ષે સ્થિતિ ઊર્જા $1 $ જૂલ હોય ત્યારે તે કેટલા ....$m$ ઉંચાઈ એ હશે ?View Solution
- 4એક અવકાશયાન કે જેનુ દળ $M$ છે. તે $V$ જેટલા વેગથી ગતિ કરે છે અને અચાનક બે ભાગમાં ફાટે છે. તેનો એક $m$ દળનો ભાગ સ્થિર લઇ જાય છે. ત્યારે બીજા ભાગનો વેગ કેટલો હશે?View Solution
- 5$2\, kg$ દળનો પદાર્થ $1\, J / s$ જેટલો અચળ પાવર આપતા એંજિન દ્વારા ચાલે છે. પદાર્થ સ્થિર સ્થિતિમાંથી શરૂ કરીને સુરેખ પથ પર ગતિ કરે છે. $9$ સેકન્ડમાં પદાર્થે કેટલા $m$ અંતર કાપશે?View Solution
- 6એક $m$ દળવાળી કાર એ એવું એન્જિન ધરાવે છે જે $P$ જેટલો પાવર પૂરો પાડી શકે છે. તો કારએ કેટલાં ન્યૂનતમ સમયમાં સ્થિર સ્થિતિમાંથી $v$ જેટલી ઝડપ સુધી પ્રવેગિત થઈ શકે છે તે...View Solution
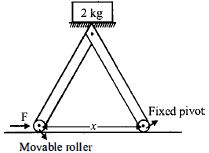
- 7બે સમાન $1\, m$ લંબાઈ ના સળિયા ધરાવતું એક મશીન આકૃતિ માં બતાવ્યા મુજબ ટોચ પર ધરી દ્વારા જોડેલ છે. તેના એક સળિયાનો છેડો જમીન સાથે સ્થિત ધરી દ્વારા જોડેલ છે અને બીજા સળિયાનો છેડો એક રોલર સાથે જોડેલ છે જે જમીન પર એક અમુક અંતર સુધી ફરી શકે . જ્યારે રોલર આગળ પાછળ જાય છે ત્યારે $2\, kg$ નું વજનિયું ઉપર નીચે જાય છે. જો રોલર જમણી તરફ અચળ ઝડપે ગતિ કરે તો વજનિયું ઉપર તરફ .... થી ગતિ કરશે.View Solution
- 8એક કણ કે જે ફરજિયાત પણ $x-$ અક્ષ પર ગતિ કરે છે. તેના પર એ જ દિશામાં એક બળ લગાવવામાં આવે છે કે જે ઉગમબિંદુથી કણના અંતર $x$ સાથે $F(x) = -kx + ax^3$ અનુસાર બદલાય છે. જ્યા $k$ અને a ઘન અચળાંક છે. $x \ge 0$માટે પદાર્થની સ્થિતિ ઊર્જા $U (x)$ નો આલેખ કેવો હશે ?View Solution
- 9$m$ દ્રવ્યમાનને એક પાતળા તાર સાથે જોડેલ છે અને તેને શિરોલંબ વર્તુળમાં ફેરવવામાં આવે છે. આ તાર મોટા ભાગે તૂટી જશે જ્યારેView Solution
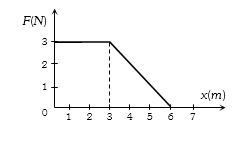
- 10એક પદાર્થ પર લાગતું બળ $F$, તેના સ્થાનાંતર $x$ સાથે આકૃતિમાં દર્શાવ્યા મુજબ બદલાય છે. બળ ન્યુટનમાં અને $x$ મીટરમાં છે. $x=0$ થી $x = 6\; m$ સુધી પદાર્થની ગતિ માટે બળ દ્વારા કેટલું કાર્ય ($J$ માં) થયું હશે?View Solution
