$l$ લંબાઇની દોરી પર પદાર્થ લટકાવેલ છે,પદાર્થના નીચેના બિંદુએ કેટલો મહત્તમ વેગ આપવાથી મહત્તમ ઊંચાઇએ તણાવ શૂન્ય થાય ?
Medium
c
(c) \(T+m g=\frac{m v_{1}^{2}}{l}\)v
(c) \(T+m g=\frac{m v_{1}^{2}}{l}\)v
There is certain velocity so called as critical velocity/minimum velocity (v) of object at highest point below which string become slack le. tension T vanishes (T=0).
\(m g=\frac{m v_{1}^{2}}{l}\)
\(v_{1}=\sqrt{g l}\)
The decrease in potential energy between top \(-\)position and bottom position is
\(m g l-(-m g l)=2 m g l\)
This must be equal to the increase in kinetic energy, when particle move from highest point
i.e.
\(\frac{1}{2} m v_{2}^{2}-\frac{1}{2} m v_{1}^{2}\)
Using law of conservation of energy.
\(2 m g l=\frac{1}{2} m v_{2}^{2}-\frac{1}{2} m v_{1}^{2}\)
\(2 m g l=\frac{1}{2} m v_{2}^{2}-\frac{1}{2} m g l\)
\(4 m g l=m v_{2}^{2}-m g l\)
\(v_{2}^{2}=5 g l\)
\(v_{2}=\sqrt{5 g l}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\mathrm{m}$ દળના કણને સમક્ષિતિજ સાથે $\theta=\frac{\pi}{3}$ના ખૂણે $u$ વેગથી પ્રક્ષિપ્ત કરવામાં આવે છે. જ્યારે તે મહત્તમ ઊંચાઈ પર પહોચે ત્યારે તે બીજા સમાન દળ અને $u \hat i$ વેગ ધરાવતા કણ સાથે અસ્થિતિસ્થાપક સંઘાત અનુભવે છે.બંને ભેગા દળ જમીન પર આવે ત્યાં સુધી તેણે કેટલું સમક્ષિતિજ અંતર કાપ્યું હશે?View Solution
- 2$20 kg$ નો પદાર્થ $ 10 m/s $ ની ઝડપે ગતિ કરતો $5 kg$ ના સ્થિર પદાર્થ સાથે અથડાય છે. અથડામણ બાદ બન્ને પદાર્થ ચોંટી જાય છે. તો તેમની સંયુકત ગતિઊર્જા …… $J$ થશે.View Solution
- 3એક માણસની ગતિઊર્જા તેનાથી અડઘું દળ ઘરાવતા છોકરાથી અડઘી છે.જો માણસની ઝડપમાં $ 1 m/s$ નો વઘારો કરવામાં આવે તો બંનેની ગતિઊર્જા સમાન થાય છે. માણસની મૂળ ઝડપView Solution
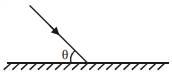
- 4$u$ ઝડપ સાથે ગતિ કરતો .... દળનો દડોએ આકૃતિમાં દર્શાવ્યા મુજબ લીસી સમક્ષિતિજ સપાટી સાથે $\theta$ ખૂણે અથડામણ અનુભવે છે. દડા વડે સપાટી પર લાગતા આઘાતની માત્રા કેટલી છે. અથડામણનો રેસ્ટીટ્યુશન અંક $e$ છે]View Solution
- 5View Solutionએક કણ પર લાગતા બળનું મૂલ્ય અચળ છે અને તે તેના વેગને લંબરૂપે લાગે છે.પરિણામે કણ એક સમતલમાં ગતિ કરે છે,તો કહી શકાય કે...
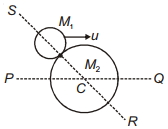
- 6એક $M_1$ દળનો પદાર્થ $u$ ઝડપે સમક્ષિતિજ ગતિ કરી રહેલો પદાર્થ સ્થિર સ્થિતિમાં રહેલાં $M_2$ દળના બીજા પદાર્થ સાથે સ્થિતિસ્થાપક અથડામણ અનુભવે છે. સાયું વિધાન પસંદ કરો.View Solution
- 7$10 m $ ઉંચાઈએથી એક બોલને ફેંક્યા પછી તે અધોદીશામાં $1 m/s $ ના વેગથી ઉતરાણ કરતી લીફટની છત પર અથડાય છે. તો બોલનો પ્રત્યાઘાતી વેગ કેટલા ....$m/s$ હશે ?View Solution
- 8View Solutionહલકા પદાર્થ અને ભારે પદાર્થની ગતિ ઊર્જા સમાન છે. તો વેગમાનનું મૂલ્ય શું હશે ?
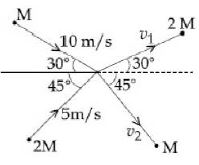
- 9$M$ અને $2M$ દળ અને $10\, m/s$ અને $5\, m/s$ વેગ ધરાવતા બે કણ ઉગમબિંદુ પાસે સ્થિતિસ્થાપક અથડામણ અનુભવે છે.અથડામણ પછી બંને આકૃતિમાં દર્શાવ્યા મુજબ $v_1$ અને $v_2$ વેગથી ગતિ કરે તો $v_1$ અને $v_2$ અનુક્રમે કેટલા મળે?View Solution
- 10$M $ દળનો બ્લોક $ K$ બળ અચળાંક ધરાવતી સ્પિંગ્ર સાથે અથડાવાથી સ્પિંગ્રનું સંકોચન $ L$ થાય છે.તો બ્લોકનું અથડામણ પછીનું મહત્તમ વેગમાન કેટલું થાય?View Solution

