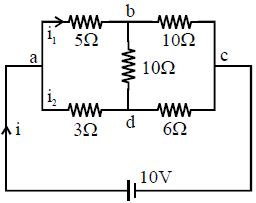
This is a balanced wheatstone bridge circuit. Therefore, we can drop \(10 \,\Omega\) resistance across points band d for the further analysis of the bridge. In This case, combination of resistances in upper and lower branches are in series with equivalent resistances \(15 \,\Omega\) and \(9 \,\Omega\) respectively. These equivalent resistances are connected in parallel across junction \(\mathrm{a}\) and \(\mathrm{c}.\) Thus equivalent resistance of the circuit \(-\)
\(\frac{1}{\mathrm{R}_{\mathrm{eq}}}=\frac{1}{15}+\frac{1}{9}\) or \(\quad \mathrm{R}_{\mathrm{eq}}=\frac{(15)(9)}{15+9}=\frac{135}{24}=5.62\, \Omega\)
Current through circuit i \(=\frac{10}{5.62}=1.78 \mathrm{\,A}\)
If current through upper and lower branches of the network are \(\mathrm{i}_{1}\) and \(\mathrm{i}_{2}\), then according to Kirchoff's function law \(-\)
\(\mathrm{i}_{1}+\mathrm{i}_{2}=1.78 \mathrm{\,A}\)
and \(\left(\mathrm{V}_{\mathrm{a}}-\mathrm{V}_{\mathrm{b}}\right)+\left(\mathrm{V}_{\mathrm{b}}-\mathrm{V}_{\mathrm{c}}\right)=\left(\mathrm{V}_{\mathrm{a}}-\mathrm{V}_{\mathrm{d}}\right)+\left(\mathrm{V}_{\mathrm{d}}-\mathrm{V}_{\mathrm{c}}\right)\)
or \(\quad \mathrm{i}_{1}(5+10)^{3 / 4}\, \mathrm{i}_{2}(3.0+6.0)\) or \((15) \mathrm{i}_{1}=(9.0) \mathrm{i}_{2}\)
On solving, we get \(-\) \(\mathrm{i}_{1}=0.67 \mathrm{\,A}\) and \(\mathrm{i}_{2}=1.1 \mathrm{\,A}\)
Download our appand get started for free
Similar Questions
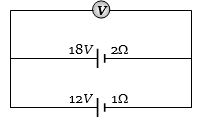
- 1આકૃતિમાં દર્શાવ્યા મુજબ $18\,volts$ $ emf$ અને $2\,\Omega $ આંતરિક અવરોધ ધરાવતી બેટરીને બીજી $12\,volts$ $ emf$ અને $1\,\Omega $ આંતરિક અવરોધ ધરાવતી બેટરી સાથે જોડેલ છે. વોલ્ટમીટર $V$ નું અવલોકન ......... $volt$ થાય.View Solution
- 2એક ઈલેકટ્રોન $10\ cm.$ ત્રિજ્યાના વર્તૂળ પર $4 \times 10^6 \,m/sec$ ની અચળ ઝડપથી ગતિ કરે છે વર્તૂળ પરના કોઈ બિંદુએ વિધુતપ્રવાહ શોધો.View Solution
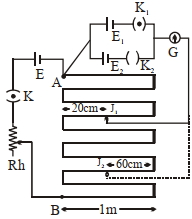
- 3આપેલ પોટેન્શીયોમીટર પરિપથમાં, $AB (10\, m$ લંબાઈ) ને સમાંતર સ્થિતિમાન $E$ એ $E_1$ અને $E_2$ કરતાં પણ વધારે છે. કળ $K_1$ (બંધ), જોકી (કળ) ને એવી રીતે બિંદુ $J_1$ આગળ ગોઠવવામાં આવે છે કે જેથી ગેલ્વેનોમીટરમાં આવર્તન ના મળે. હવે $K_1$ ને ખુલ્લી કરીને પ્રથમ બેટરી $(E_1)$ ને બદલે બીજી બેટરી $(E_2)$ જોડવામાં આવે છે, જ્યારે $K_2$ બંધ છે. હવે ગેલ્વેનોમીટર $J_2$ સ્થાન માટે શૂન્ય કોણાવર્તન આપે છે $\frac{ E _{1}}{ E _{2}}$ નું મૂલ્ય $\frac{ a }{ b }$ થશે જ્યાં $a=.............$ છે.View Solution
- 4એક મોટા મકાનમાં $40$ $W$ ના $15$ ગોળા,$100$ $W $ ના $5$ ગોળા,$80$ $W$ નાં $5$ પંખા અને $1$ $kW$ નું $1$ ઉષ્ણક (હીટર) છે. વિદ્યુત ઉદ્ગમનો સ્થિતિમાન $220$ $ V $ છે,તો મકાનનો લઘુત્તમ ક્ષમતા ધરાવતો ફયુઝ ................. $A$ નો હશે.View Solution
- 5આંતરિક અવરોધ $r$ ધરાવતી બેટરી સાથે $R$ અવરોધ જોડેલ છે $R$ અવરોધ પર મહત્તમ પાવર કરવા માટે ...View Solution
- 6ચોરસ લૂપ બનાવવા માટે $16\, \Omega$ વાળા તારને વાળવામાં આવે છે. તેની એક બાજુ સાથે $9 \,{V}$ અને $1 \,\Omega$ નો આંતરિક આંતરિક અવરોધ ધરાવતા સ્ત્રોતને જોડવામાં આવે છે. ચોરસ લૂપના કર્ણ વચ્ચે વિદ્યુત સ્થિતિમાનનો તફાવત $.......\,\times 10^{-1} \,{V}$ હશે.View Solution
- 7$E_1$ અને $E_2$ $emf$ના બે કોષો $\left(E_1 > E_2\right)$ ને સ્વતંત્ર રીતે પોટેન્શીયમીટર સાથે જોંડામાં આવે છે. અને તેમને અનુરૂપ બેલેન્સીંગ લંબાઈ $625\,cm$ અને $500\,cm$ હોય,તો $\frac{E_1}{E_2}$ ગુણોતર કેટલો છે.View Solution
- 8એક પોલા નળાકાર વાહકની લંબાઇ $3.14\,m$ છે જ્યારે તેની આંતરિક અને બાહ્ય વ્યાસ અનુક્રમે $4\,mm$ અને $8\,mm$ છે.વાહકનો અવરોધ $n \times 10^{-3}\,\Omega$ છે.જો દ્રાવ્યની અવરોધકતા $2.4 \times 10^{-8}\,\Omega m$ હોય તો $n$ નું મૂલ્ય $............$ છે.View Solution
- 9એક મીટરબ્રીજમાં, $1\,m$ લંબાઈનો તાર અસમાન આડછેદ એવી રીતે ધરાવે છે કે તેના અવરોધ $R$ નો લંબાઈ $l$ સાથેનો ફેરફાર $\frac{{dR}}{{d\ell }} \propto \frac{1}{{\sqrt \ell }}$ છે. આકૃતિમાં બતાવ્યા પ્રમાણે બે સમાન અવરોધો જોડેલ છે. જ્યારે જોકી એ બિંદુ $P$ પર હોય ત્યારે ગેલ્વેનોમીટરમાં આવર્તન શૂન્ય છે. લંબાઈ $AP$ કેટલા .................. $m$ હશે?View Solution
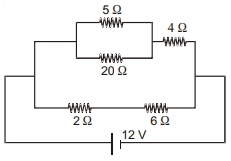
- 10પાંચ અવરોધો ધરાવતા એક પરિપથને $12\,V\,emf$ સાથે. બેટરી સાથે આકૃતિમાં દર્શાવ્યા મુજબ જોડલ છે. તો $4\,\Omega$ અવરોધની વચ્ચે વિદ્યુત સ્થિતિમાનનો તફાવત $.........V$ છે.View Solution