આકૃતિમાં દર્શાવ્યા અનુસાર, $M$ દળ ધરાવતા અને $R$ ત્રિજયા ધરાવતા ઘન ગોળામાંથી $\frac{R}{2}$ ત્રિજયા ધરાવતો ગોળાકાર ભાગ દૂર કરવામાં આવેલ છે.$r$ $=$ $\;\infty $ અંતરે ગુરુત્વીય સ્થિતિમાન $V=0 $ લઇ,ગોળામાંથી દૂર કરેલા ભાગ (કેવિટી ) ના કેન્દ્ર આગળ સ્થિતિમાન __________ થશે. ( $G$ $=$ ગુરુત્વાકર્ષી અચળાંક )
JEE MAIN 2015, Diffcult
Download our app for free and get started
a
Due to complete solid sphere, potential at point \(p\)
Due to complete solid sphere, potential at point \(p\)
\({V_{sphere}} = \frac{{ - GM}}{{2{R^3}}}\left[ {3{R^2} - {{\left( {\frac{R}{2}} \right)}^2}} \right]\)
\( = \frac{{ - GM}}{{2{R^3}}}\left( {\frac{{11{R^2}}}{4}} \right) = - 11\frac{{GM}}{{8R}}\)
Due to cavity part potential at point \(P\)
\({V_{cavity}} = - \frac{3}{2}\frac{{\frac{{GM}}{8}}}{{\frac{R}{2}}} = - \frac{{3GM}}{{8R}}\)
So potential at the center of carvity
\( = {V_{sphere}} - {V_{cavity}} = - \frac{{11GM}}{{8R}} - \left( { - \frac{3}{8}\frac{{GM}}{R}} \right)\)
\( = \frac{{ - GM}}{R}\)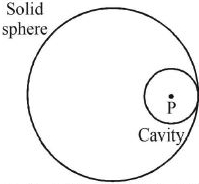
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionધ્રુવ અને વિષુવવૃત ના ગુરુત્વ પ્રવેગ વચ્ચેનો સંબંધ
- 2View Solutionવિધાન : અવકાશ રોકેટ મોટા ભાગે પશ્ચિમથી પૂર્વ તરફ જતી વિષુવવૃત્તીય રેખા પરથી પ્રક્ષેપ કરવામાં આવે છે.
કારણ : વિષુવવૃત્ત પર ગુરુત્વપ્રવેગનું મૂલ્ય સૌથી ઓછું હોય.
- 3View Solutionજો પૃથ્વી સંકોચાય ને તેની ત્રિજ્યા અડધી થય જાય પણ દળ સમાન રહે તો ગુરુત્વ પ્રવેગનું મૂલ્ય કેટલું થાય?
- 4પૃથ્વીની સપાટી પર પદાર્થનું વજન $72 \,N$ છે. જો તેને $h=2 R$ ઊંચાઈ એ લઈ જવામાં આવે, તો તેનું વજન ........... $N$ હશે ?View Solution
- 5પૃથ્વીની સપાટીથી $h$ ઊંચાઈ પર એક ઉપગ્રહ વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે કે જ્યાં $h < < R$ અને $R$ પૃથ્વીની ત્રિજ્યા છે. પૃથ્વીના વાતાવરણની અસરને અવગણતા, પૃથ્વીના ગુરૂત્વાકર્ષણ ક્ષેત્રમાંથી છટકવા ઝડપમાં જરૂરી લઘુત્તમ વધારો ______ કરવો પડે.View Solution
- 6બે ગ્રહ પૃથ્વીની ફરતે ફરે છે જેના વેગ $v_1$ અને $v_2$ છે જો તેની કક્ષીય ત્રિજ્યા $r_1$ અને $r_2$ ($r_1>r_2$) હોય તો ...View Solution
- 7પ્રત્યેક $ ‘M’$ દળ ધરાવતા ચાર કણો એકબીજાથી એકસરખા અંતરે $R$ ત્રિજયા ધરાવતા વર્તુળ પર તેમના અન્યોન્ય ગુરુત્વ આકર્ષણ બળની અસર હેઠ ગતિ કરે છે,તો દરેક કણની ઝડપView Solution
- 8$M$ દળ અને $R$ ત્રિજ્યાના પોલા ગોળાના કેન્દ્રથી $r$ અંતરે $m$ દળનો કણ પડેલો છે.તો ગુરુત્વસ્થિતિઉર્જા $ U\,(r)$ વિરુદ્ધ $r$ નો ગ્રાફ નીચે પૈકી કયો થાય?View Solution
- 9બે તારાના તંત્રમાં $m_{A}$ અને $m_{B}$ દળ ધરાવતા બે તારા $A$ અને $B$ અનુક્રમે $r_{A}$ અને $r_{B}$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં ગતિ કરે છે. જો $T_{A}$ અને $T_{B}$ અનુક્રમે તારો $A$ અને તારા $B$ નો આવર્તકાળ હોય, તો .....View Solution
- 10પૃથ્વીની સપાટી પર ગુરૂત્વપ્રવેગ $g$ છે. જો પૃથ્વીનો વ્યાસ ઘટીને તેના મૂળ મૂલ્ય કરતા અડધો થાય અને દળ અચળ રહે તો પૃથ્વીની સપારી પરનો ગુરૂત્વપ્રવેગ_______થશે.View Solution