આકૃતિમાં દર્શાવ્યા મુજબ $5\, cm$ પાણીથી ભરેલા ગ્લાસના તળિયે $40\, cm$ વક્રતા ત્રિજ્યા ધરાવતો અંતર્ગોળ અરીસો છે.પાણીની સપાટી પર એક નાના કણનું પ્રતિબિંબ ગ્લાસની ઉપર પાણીની સપાટીથી $d$ અંતરે મળે તો $d$ લગભગ કેટલા .....$cm$ હશે?
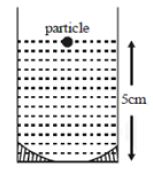

JEE MAIN 2019, Diffcult
b
Light incident from particle \(P\) will be reflected at mirror.
Light incident from particle \(P\) will be reflected at mirror.
\({\text{u}} = - 5\,{\text{cm}},\) \({\text{f}} = {\text{m}} - \frac{{\text{R}}}{2}\) \( = - 20\,{\text{cm}}\)
\(\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\) ; \(\boxed{{v_1} = + \frac{{20}}{3}\,\,cm}\)
This image will act as object for light getting refracted at water surface.
So, object distance \(d=5+\frac{20}{3}=\frac{35}{3} \,\mathrm{cm}\)
Below water surface.
After refraction, final image is at
\({d^\prime } = d\left( {\frac{{{\mu _2}}}{{{\mu _1}}}} \right)\) \( = \left( {\frac{{35}}{3}} \right)\left( {\frac{1}{{4/3}}} \right)\)
\(=\frac{35}{4}=8.75 \,\mathrm{cm}\)
\( \approx 8.8\, \mathrm{cm}\)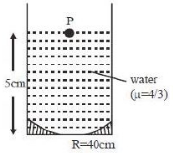
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પાત્રમાં આકૃતિ મુજબ પ્રવાહી ભરેલા છે. $1.61$ વક્રીભવનાંક ધરાવતા કાંચના ટુકડાને નાખતાં તે ,કયાં પ્રવાહીમાં દેખાશે નહિ?View Solution

- 2${f_1}$ અને ${f_2}$ કેન્દ્રલંબાઇ ધરાવતા બે પાતળા લેન્સને સંપર્કમાં અને સમઅક્ષીય મૂકેલા છે. તંત્ર કેટલા પાવરના એક લેન્સને સમતુલ્ય થાય?View Solution
- 3$44\,cm$ લંબાઈ ધરાવતા એસ્ટ્રોનોમિકલ ટેલિસ્કોપની કોણીય મોટવણી $10$ છે. ઓબ્જિેકિટવની કેન્દ્રલંબાઇ ($cm$ માં) કેટલી હશે?View Solution
- 4પ્રકાશનું કિરણ અને સમક્ષિતિજ સાથે $10°$ ખૂણો બનાવે છે. સમતલ અરીસો સમક્ષિતિજ સાથે $\theta$ ખૂણો બનાવે તેના પર આપાત થાય છે પરાવર્તિત કિરણ શિરોલંબ ઉર્ધ્વ દિશામાં જતું હોય, તો $\theta$ =.....$^o$View Solution
- 5બહિર્ગોળ લેન્સના એક પ્રયોગમાં, પ્રતિબિંબ અંતર $(v')$ વિરુદ્ધ કેન્દ્રથી મપાયેલ વસ્તુ અંતર $(\mu ')$ માટે $v'\mu '=225$ આપે છે. જો બધા જ અંતરો $cm$ એકમમાં માપતા હોય તો લેન્સની કેન્દ્રલંબાઈનું મૂલ્ય $...........cm$ થશે.View Solution
- 6$+ 15\, cm, + 20\,cm, + 150\,cm$ અને $+ 250\, cm$ કેન્દ્રલંબાઈ ધરાવતા લેન્સથી એસ્ટ્રોનોમિકલ ટેલિસ્કોપ બનાવવામાં આવે છે. મોટવણી મહતમ કરવા માટે આઇપીસની કેન્દ્રલંબાઈ ........ $cm$View Solution
- 7બે $40°$ ખૂણે રહેલા અરીસા દ્વારા કિરણનું સફળતાથી પરાવર્તન થાય છે. જો પ્રથમ અરીસા પર આપાત કોણ $30°$ હોય ત્યારે કિરણનું કુલ વિચલન .....$^o$ થશે.View Solution
- 8એસ્ટ્રોનોમિકલ ટેલિસ્કોપની મોટવણી $5$ છે,ઓબ્જિેકિટવપીસ અને આઇપીસ વચ્ચેનું અંતર $36cm$ છે. તો ઓબ્જિેકિટવપીસ $f_o$ અને આઇપીસ $f_e$ ની કેન્દ્રલંબાઇ કેટલી હશે?View Solution
- 9$2 \mathrm{h}$ ઊંચાઈ ધરાવતા પાત્રનો નીચેનો અડધો ભાગ $2 \sqrt{2}$ અને ઉપરનો અડધો ભાગ $\sqrt{2}$ વક્રીભવનાંકવાળા પ્રવાહીથી ભરેલો છે.બંને પ્રવાહી એકબીજામાં મિશ્ર થતાં નથી. તો પાત્રનું તળિયું કેટલી ઊંચાઈ પર દેખાશે?View Solution
- 10સંયુકત માઇક્રોસ્કોપમાં ઓબ્જિેકિટવપીસ અને આઇપીસની મોટવણી $m_1$ અને $m_2$ છે.તો સંયુકત માઇક્રોસ્કોપની મોટવણી કેટલી થાય?View Solution
