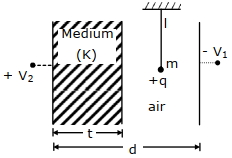
Let \(E\) be electric field in air
\(T \sin \theta=q E\)
\(T \cos \theta=m g\)
\(\tan \theta=\frac{q {E}}{m g}\)
\({Q}=\left[\frac{{C}_{1} {C}_{2}}{{C}_{1}+{C}_{2}}\right]\left[{V}_{1}+{V}_{2}\right]\)
\({E}=\frac{{Q}}{{A} \in_{0}}=\left[\frac{{C}_{1} {C}_{2}}{{C}_{1}+{C}_{2}}\right] \frac{\left[{V}_{1}+{V}_{2}\right]}{{A} \in_{0}}\)
\({C}_{1}=\frac{\epsilon_{0} {A}}{{d}-{t}} \Rightarrow {E}=\frac{{C}_{2}\left[{V}_{1}+{V}_{2}\right]}{\left({C}_{1}+{C}_{2}\right)({d}-{t})}\)
Now \(\theta=\tan ^{-1}\left[\frac{{q} \cdot {E}}{{mg}}\right]\)
\(\theta=\tan ^{-1}\left[\frac{{q}}{{mg}} \times \frac{{C}_{2}\left({V}_{1}+{V}_{2}\right)}{\left({C}_{1}+{C}_{2}\right)({d}-{t})}\right]\)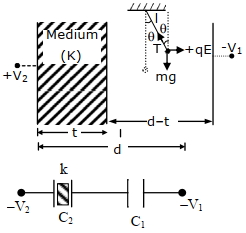
Download our appand get started for free
Similar Questions
- 1કણ $A$ અને કણ $B$ એ બંને $+ q$ અને $+ 4q$ વિદ્યુતભારો ધરાવે છે. તે બંનેના દળ $m$ છે. તેમને સ્થિર સ્થિતિમાંથી સમાન $p.d$ હેઠળ પડવા દેતા તેમના વેગનો ગુણોત્તર $v_A/v_B =$ .......View Solution
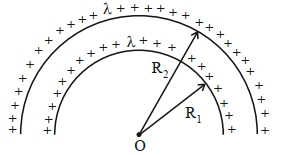
- 2સમાન રેખીય વીજભાર ધનતા $\lambda$ ધરાવતી $R _1$ અને $R _2$ ત્રિજયાની સમકેન્દ્રિય અર્ધલયોના કેન્દ્ર સ્થાને વિદ્યુત સ્થિતિમાન $.............$ છે.View Solution
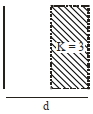
- 3$A$ જેટલો પ્લેટનું ક્ષેત્રફળ, પ્લેટો વચ્યેનું અંતર $d =2 \,m$ ધરાવતા એક સમાંતર પ્લેટ સંધારકની સંધારકતા $4 \,\mu F$ છે. જો પ્લેટો વચ્ચેના અડધા વિસ્તારને $K =3$ જેટલો ડાયઈલેકટ્રીક ધરાવતા અવાહક માધ્યમથી ભરવામાં આવે (આફૃતિ જુઓ) તો આ તંત્રની નવી સંધારકતા ......... $ \mu F$ થશે.View Solution
- 4$10^{-6} \mu \mathrm{C}$ નો એક વીજભાર $X-Y$ યામ પધ્ધતિના ઉગમબિંદુ $(0,0) \mathrm{m}$ પર મૂકેલો છે. બિંદુઓ $\mathrm{P}$ અને $\mathrm{Q}$ અનુક્રમે $(\sqrt{3}, \sqrt{3}) \mathrm{m}$ અને $(\sqrt{6}, 0) \mathrm{m}$ પર રહેલા છે. બિંદુઓ$\mathrm{P}$ અને $\mathrm{Q}$ વચચેનો સ્થિતિમાન તફાવત_____થશે.View Solution
- 5$10^{3 }\ m$ વ્યાસ ધરાવતો ધાતુ ગોળાના સ્વરૂપમાં એક રેડિયો એકટિવ પદાર્થ પ્રતિ સેકન્ડે $6.25 \times 10^{10}$ કણોના અચળ દરે કણોનું ઉત્સર્જન કરે છે. જો વાહક વિદ્યુતીય રીતે અલગ કરેલો હોય, તો તેનો સ્થિતિમાન $1.0$ વોલ્ટ, વધારવા માટે કેટલો સમય લેશે? $80\%$ ઉત્સર્જિત કણો સપાટી પરથી બહાર નીકળે છે. તેમ ધારો.......$\mu s$View Solution
- 6$5\times 10^{-9}\,C$ ના બિંદુવત વીજભારને લીધે $P$ બિંદુએ વિદ્યુત સ્થિતિમાન $50\,V$ છે. બિંદુવત વીજભારથી $P$ નું અંતર ........$cm$ છે. $\left[\frac{1}{4 \pi \varepsilon_0}=9 \times 10^{+9}\,Nm ^2\, C ^{-2}\right.$ ધારો $]$View Solution
- 7એક બિંદુ $(x,y,z) $ આગળનું વિદ્યુતસ્થિતિમાન $V=-x^2y-xz^3 +4 $ છે.આ બિંદુ એ વિદ્યુતક્ષેત્રની તીવ્રતા _______View Solution
- 8વિદ્યુતભારીત ધાતુ માટે નીચેના પૈકી કયુ વિધાન હંમેશા સાચું હોય છે?View Solution
$(1)$ પૃષ્ઠની બહારની બાજુએ વિદ્યુતક્ષેત્ર એ પૃષ્ઠને સમાંતર હશે.
$(2) \,E_{in} = 0\,\,$
$ (3)$ વિદ્યુત ક્ષેત્ર રેખાઓ સમસ્થિતિમાન પૃષ્ઠને લંબ હોય છે.
- 9View Solutionકેપેસિટરને બેટરી સાથે જોડી રાખીને તેની પ્લેટો વચ્ચે ડાઈ ઈલેકટ્રીક સ્તર મૂકવામાં આવે ત્યારે આ પ્રક્રિયામાં ........
- 10$5\, \mu F$ કેપેસીટરને $220\,V$ વડે સંપૂર્ણ ચાર્જ કરેલ છે. પછી તેને તેમાંથી અલગ કરી તેને $2.5\;\mu F$ ના બીજા વિજભારરહિત કેપેસીટર સાથે શ્રેણીમાં જોડવામાં આવે છે. જો તેના પરના વિજભારના પુનર્વિતરણ દરમિયાન તેની ઊર્જામાં થતો ફેરફાર $\frac{ X }{100}\; J$ હોય તો $X$ નું મૂલ્ય નજીકતમ પૂર્ણાંકમાં કેટલું હશે?View Solution
