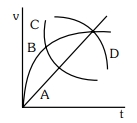
આકૃતિમાં દર્શાવ્યા મુજબ $\rho$ ઘનતા ધરાવતા પ્રવાહીથી ભરેલું પાત્ર દર્શાવે છે. ચાર બિંદુુઓ $A, B, C$ અને $D$ એ આકૃતિમાં દર્શાવ્યા મુજબ વર્તુળના વિરુદ્ધ વ્યાસાં બિંદુુઓ પર છે. $A$ અને $C$ બિંદુઓ શિરોલંબ રેખા પર રહેલા છે અને $B$ અને $D$ બિંદુુઓ સમક્ષિતિજ રેખા પર રહેલા છે. ખોટું નિવેદન પસંદ કરો. ( $p_A,p_B, p_C, p_D$ એ અનુક્કમિત બિંદુઓ પરનું $A$ નિરપેક્ષ દબાણ છે.

Diffcult
c
(c)
(c)
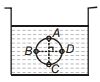
Points at same height have same pressure, points with height difference say ' \(h\) ' will have difference of \(\rho g h\).
Let radius of circle is \(r\)
\(p_A=p_0+h \rho g\)
\(p_B=p_D=p_0+(h+r) \rho g\)
\(p_C=p_0+(h+2 r) \rho g\)
Then,
\(p_C+p_A=\left[p_0+(h+2 r) \rho g\right]-\left[p_0+h \rho g\right]\)
\(=p_0+h \rho g+2 r \rho g+p_0+h \rho g\)
\(=2\left[p_0+(h+r) \rho g\right]\)
\(\frac{p_C+p_A}{2}=p_0+(h+r) \rho g\)
\(\frac{p_C+p_A}{2}=p_B=p_D\)
i.e., option \((a), (b)\) and \((d)\) gives correct statement but incorrect statement is \((c)\)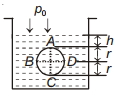
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$M$ દળ ધરાવતા અને $d$ જેટલી ઘનતા ધરાવતા એક નાના બોલ (દડા) ને, ગ્લીસરીન ભરેલા પાત્રમાં પતન કરવામાં આવે છે ત્યારે તેની ઝડપ અમુક સમય બાદ અચળ થાય છે. જે ગ્લિસરીનની ધનતા $\frac{\mathrm{d}}{2}$ જેટલી હોય તો દડા પર લાગતું સ્નિગ્ધતા (શ્યાનતા) બળ $....$ હશે.View Solution
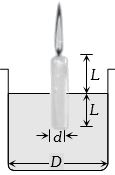
- 2$d$ વ્યાસ ધરાવતી મીણબત્તીને આકૃતિમાં દર્શાવ્યા પ્રમાણે $D (D > > d)$ વ્યાસ ધરાવતા પાત્રમાં મુકેલ છે.જો મીણબત્તી $2\, cm/hour$ ના દરથી બળતી હોય તો મીણબત્તીનો ઉપરનો ભાગ .....View Solution
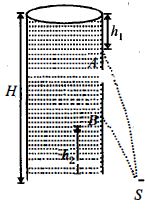
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે નળાકાર ટાંકીની દીવાલમાં $A$ અને $B$ સપાટીથી $h_1$ ઊંડાઈ અને તળિયેથી $h_2$ ઊંચાઈ પર બે હૉલ છે.પાણીની સપાટી ટાંકીના તળિયેથી $H$ ઊંચાઈ પર છે.બંને હૉલમાંથી આવતું પાણી જમીન પર સમાન સ્થાન $S$ પર પડે છે તો $h_1$ અને $h_2$ નો ગુણોત્તર કેટલો થાય?View Solution
- 4$H$ ઊંચાઈ અને $\rho$ ઘનતા ધરાવતા ટેન્કમાં પ્રવાહી ભરવામાં આવે છે. તો આ કન્ટેનરની દીવાલ પર લાગતું સરેરાશ દબાણ.View Solution
- 5એક $H$ ઊંચાઈના મોટા પાતને, $\rho$ ઘનતાના પ્રવાહીથી છલોધલ ભરવામાં આવે છે. તેની શિરોલંબ બાજુની સપાટી પર $r$ ત્રિજ્યાનું એક નાનું છિદ્ર બનાવવામાં આવે છે. (તળિયાની એકદમ નજીક) તો પ્રવાહીના દબાણને રોકવા માટે જરરી સમક્ષિતિજ બળ કેટલું હશે ?View Solution
- 6View Solutionઆકૃતિમાં દર્શાવેલ નળીમાં પ્રવાહીનું વહન થાય છે.તો દબાણ વિરુધ્ધ અંતરનો આલેખ મેળવો ?
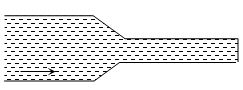
- 7$2 \,cm$ અને $4\, cm$ ત્રિજયા ધરાવતી બે નળીને શ્રેણીમાં જોડતાં તેમાં પ્રવાહનો ગુણોત્તરView Solution
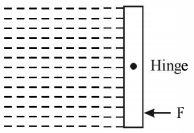
- 8$1\,m \times 1\,m$ $size$ નો ચોરસ ગેટ તેના મધ્યબિંદુથી લટકાવેલ છે.$\rho$ ઘનતાનું પ્રવાહી ગેટની ડાબી બાજુની જગ્યામાં ભરેલ છે. તો ગેટને સ્થિર રાખવા માટે જોઈતું બળ $F . \ldots . .. ....$View Solution
- 9View Solutionસાચું બર્નોલીનું સમીકરણ. . . . . . .છે. (સંજ્ઞાઓ તેમનો પ્રમાણિત અર્થ રજૂ કરે છે.)
- 10એક ગોળાકાર બોલને ખુબજ સ્નિગ્ધ પ્રવાહીના લાંબા સ્તંભમાં મુક્ત (છોડવામાં)કરવામાં આવે છે.આકૃતિમાં દર્શાવેલ વક્ર,કે જે બોલ માટે ઝડપ $(v)$ અને સમય $(t)$ના વિધેય તરીકે દર્શાવે તે$........$છે.View Solution