આકૃતિમાં દર્શાવ્યા પ્રમાણે બે આદર્શ ડાયપોલ $A$ અને $B$ જેની ડાયપોલ મોમેન્ટ અનુક્રમે $p_{1}$ અને $p_{2}$ છે, તેને સમતલમાં તેના કેન્દ્ર $O$ પર રહે તેમ મુકેલ છે. ડાયપોલ $A$ ની અક્ષ પરના બિંદુ $C$ પર, પરિણામી વિદ્યુતક્ષેત્ર અક્ષ સાથે $37^{\circ}$ ની ખૂણો બનાવે છે. $A$ અને $B$ ની ડાયપોલ મોમેન્ટ નો ગુણોત્તર, $\frac{P_{1}}{P_{2}}$ કેટલો થાય?
($\sin 37^{\circ}=\frac{3}{5}$ લો)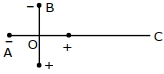
JEE MAIN 2021, Diffcult
b
\(\tan 37^{\circ}=\frac{3}{4}=\frac{\frac{ kP _{2}}{ r ^{3}}}{\frac{2 kP _{1}}{ r ^{3}}}=\frac{ P _{2}}{2 P _{1}}=\frac{3}{4}\)
\(\tan 37^{\circ}=\frac{3}{4}=\frac{\frac{ kP _{2}}{ r ^{3}}}{\frac{2 kP _{1}}{ r ^{3}}}=\frac{ P _{2}}{2 P _{1}}=\frac{3}{4}\)
\(\frac{ P _{2}}{ P _{1}}=\frac{3}{2}\)
\(\frac{ P _{1}}{ P _{2}}=\frac{2}{3}\)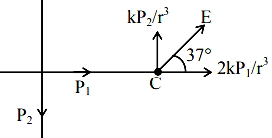
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન વિદ્યુતક્ષેત્ર $\overrightarrow {\;E} $ ની અસર નીચે સમક્ષિતિજ $q$ વીજભારિત એક રમકડાંની કાર ઘર્ષણરહિત સપાટ સમક્ષિતિજ સમતલ પર ગતિ કરે છે.બળ $q \overrightarrow {\;E} $ ના કારણે એક સેકન્ડના ગાળામાં તેનો વેગ $0$ થી $6 \,m/s$ વધે છે. આ ક્ષણે આ ક્ષેત્રની દિશા ઉલટાવવામાં આવે છે. આ ક્ષેત્રની અસરમાં આ કાર બે સેકન્ડ ગતિ કરવાનું ચાલુ રાખે છે. $0$ થી $3$ સેકન્ડ વચ્ચે રમકડાની આ કારનો સરેરાશ વેગ અને સરેરાશ ઝડપ અનુક્રમે કેટલી હશે?View Solution
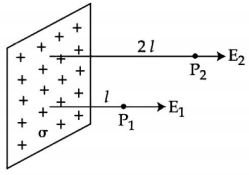
- 2આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરોView Solution
- 3એકબીજાથી $\mathrm{rcm}$ અંતરે આવેલા બે બિંદુવતત વિદ્યુતભારો $\mathrm{q}_1$ અને $\mathrm{q}_2$ વચ્ચે લાગતુ બળ $\mathrm{F}$ છે. જો આ બંને વિદ્યુતભારો ને $\mathrm{K}=5$ ડાય ઈલેક્ટ્રિક અચળાંક ધરાવતા માધ્યમ $\mathrm{r} / 5 \mathrm{cm}$ અંતરે મુકવામાં આવે તો તેમની વચ્ચે લાગતુ બળ ......View Solution
- 4$10\,\mu C$ વીજભારને બે ભાગમાં વિભાજીત કરીને $1\,cm$ નાં અંતરે એવી રીતે મૂકવામાં આવે છે, કે જેથી તેના પર લાગતું અપાકર્ષી બળ મહત્તમ હોય. બે ભાગના વીજભાર ......... છે.View Solution
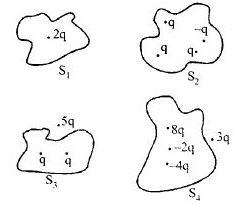
- 5ચાર સપાટી માટે વિદ્યુતભારનું વિતરણ આપેલ છે. તેમને અનુરૂપ વિદ્યુત ફ્લક્સ ${\phi _1},{\phi _2},{\phi _3}$ અને ${\phi _4}$ હોય તો નીચેનામાંથી શું સાચું પડે?View Solution
- 6$M$ દળ અને $q$ વિજભાર $k$ દળ ધરાવતી સ્પ્રિંગ સાથે જોડાયેલ છે. $x = 0$ ને સમતોલન સ્થાન રાખીને તે $x-$દિશામાં $A$ કંપવિસ્તારથી દોલનો કરે છે,$x-$દિશામાં $E$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્તે છે. તો નીચેનામાંથી કયું વિધાન સાચું પડે?View Solution
- 7$a/4$ ત્રિજ્યાની તકતી જે સમાન વિતરણ વિજભાર $6 c$ ધરાવે છે. તેને $x - y$ સમતલમા $(-a / 2,0,0)$ કેન્દ્ર સાથે તે માં મૂકવામાં આવે છે.$a$ લંબાઈનો સળિયો જે સમાન વિતરણ વીજભાર $8c$ ધરાવે છે તેને $X = a / 4$ થી $X =5 a / 4$ સુધી $X - axis$ પર મૂકેલ છે. જો બિંદુવત વીજભાર $-7 c$ અને $3 c$ ને $(a / 4,-a / 4,0)$ પર અને $(-3 a / 4,3 a / 4,0)$ પર મૂકેલ છે.બે સપાટી, $x=\pm a / 2, \quad Y =\pm a / 2, \quad Z =\pm a / 2$ દ્વારા બનતા ગોળાકાર સપાટીને ધ્યાનમાં લો. તેમાંથી પસાર થતું વિદ્યુત ફ્લક્સ $..........$View Solution
- 8$r_1$ અને $r_2$ ત્રિજ્યાની સમકેન્દ્રી રિંગ પર $Q_1$ અને $Q_2$ વિધુતભાર છે તો કેન્દ્રથી $r$ $(r_1 < r < r_2)$ અંતરે વિધુતક્ષેત્ર શોધોView Solution
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે સમાન ગતિ ઉર્જા ધરાવતા પ્રોટોન અને $\alpha$ કણ ને એકરૂપ લંબ વિદ્યુતક્ષેત્રમાં પ્રક્ષેપિત કરવામાં આવ્યા છે, તોView Solution
- 10$2 \,m$ અંતરે રહેલા બે સમાન વિદ્યુતભાર $q$ ધરાવતા બે સ્થિર કણની વચ્ચે એક $1 \,{mg}$ દળ અને $q$ વિદ્યુતભાર ધરાવતો કણ પડેલો છે. જો મુક્ત વિદ્યુતભારને તેના સમતોલન સ્થાનેથી $x\;(x\, < 1\, {m})$ જેટલું થોડુક સ્થાનાંતર કરવવામાં આવે, તો કણ સરળ આવર્ત ગતિ કરે છે. જો ${q}^{2}=10\, {C}^{2}$ હોય તો આ દોલનોની કોણીય આવૃતિ $....\,\times 10^{8}\, {rad} / {s}$ થાય.View Solution
