$2 \,m$ અંતરે રહેલા બે સમાન વિદ્યુતભાર $q$ ધરાવતા બે સ્થિર કણની વચ્ચે એક $1 \,{mg}$ દળ અને $q$ વિદ્યુતભાર ધરાવતો કણ પડેલો છે. જો મુક્ત વિદ્યુતભારને તેના સમતોલન સ્થાનેથી $x\;(x\, < 1\, {m})$ જેટલું થોડુક સ્થાનાંતર કરવવામાં આવે, તો કણ સરળ આવર્ત ગતિ કરે છે. જો ${q}^{2}=10\, {C}^{2}$ હોય તો આ દોલનોની કોણીય આવૃતિ $....\,\times 10^{8}\, {rad} / {s}$ થાય.
JEE MAIN 2021, Diffcult
b
Net force on free charged particle
Net force on free charged particle
\(F =\frac{ kq ^{2}}{( d + x )^{2}}-\frac{ kq ^{2}}{( d - x )^{2}}\)
\(F =- kq ^{2}\left[\frac{4 dx }{\left( d ^{2}- x ^{2}\right)^{2}}\right]\)
\(a =-\frac{4 kq ^{2} d }{ m }\left(\frac{ x }{ d ^{4}}\right)\)
\(a =-\left(\frac{4 kq ^{2}}{ md ^{3}}\right) x\)
So, angular frequency
\(\omega=\sqrt{\frac{4 kq ^{2}}{ md ^{3}}}\)
\(\omega=\sqrt{\frac{4 \times 9 \times 10^{9} \times 10}{1 \times 10^{-6} \times 1^{3}}}\)
\(\omega=6 \times 10^{8}\; rad / sec\)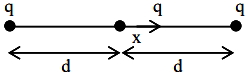
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન વિદ્યુતભાર ધરાવતા બે સમાન ગોળાઓને એક આધારબિંદુથી સરખી લંબાઈની દોરી વડે લટકાવેલ છે. ત્યારે બે દોરી વચ્ચેનો કોણ $30^o$ છે. જ્યારે $0.8\, g\, cm^{-3}$ ઘનતાના પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે બે દોરી વચ્ચેનો કોણ ગોળાઓ હવામાં હતા તયારે જેટલો હતો તેટલો જ રહે છે. જો ગોળાઓના દ્રવ્યની ઘનતા $1.6 \,g \,cm^{-3}$ હોય તો પ્રવાહીનો ડાઈઈલેક્ટ્રિક અચળાંક ........ છે.View Solution
- 2એક બંધ પૃષ્ઠની અંદર અને બહાર જતું વિદ્યુત ફલ્કસ ${\varphi _1}$ અને ${\varphi _2}$ છે.તો પૃષ્ઠની અંદર વિદ્યુતભાર કેટલો હશે?View Solution
- 3$L$ લંબાઈ અને $R$ ત્રિજ્યાનો એક નળાકાર લો કે જેની અક્ષો વિદ્યુતક્ષેત્ર ને સમાંતર હોય નળાકાર સાથે સંકળાયેલ કુલ વિદ્યુત ફલક્સ ....... છે.View Solution
- 4$p$ ડાયપોલ મોમેન્ટ ધરાવતા ડાયપોલનું કેન્દ્ર ઉદ્ગમબિંદુ પર રહે તે રીતે $x$-અક્ષ પર મૂકેલ છે.ડાયપોલના કેન્દ્રથી અમુક અંતરે આવેલા બિંદુને જોડતી રેખાએ $x$-અક્ષ સાથે બનાવેલો ખૂણો $\theta $ છે.તો તે બિંદુએ વિદ્યુતક્ષેત્રએ $x$-અક્ષ સાથે કેટલો ખૂણો બનાવે? [ $\tan \alpha = \frac{1}{2}\tan \theta $ ]View Solution
- 5જ્યારે ધાતુના તટસ્થ ગોળામાંથી $10^{14}$ ઈલેકટ્રોનસને દૂર કરવામાં આવે તો ગોળા પરનો વિદ્યુતભાર.......$\mu C$ હશે ?View Solution
- 6બે સમાન ધન બિંદુવત વિદ્યુતભારને એકબીજાથી $2a$ અંતરથી અલગ કરવામાં આવે છે. બે વિદ્યુતભારને જોડતી રેખાના કેન્દ્રથી વિષુવવૃત્તીય રેખા (લંબ દ્વિભાજક) પરના એક બિંદુનું અંતર કે જેના પર પરીક્ષણ વિદ્યુતભાર $q_0$ દ્વારા અનુભવાતું બળ મહત્તમ થાય તે $\frac{a}{\sqrt{x}}$ છે. $x$ નું મૂલ્ય કેટલું હશે?View Solution
- 7આકૃતિમાં દર્શાવ્યા અનુસારે બે બિંદુવત વિદ્યુતભારો $- q$ અને $+q$ ને $L$ જેટલા અંતરે મુકવામાં આવેલ છે.View Solution
$R ( R > > L )$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતાનું મૂલ્ય $.....$ પ્રમાણે બદલાશે.
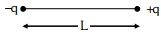
- 8$5\,\mu C$ બિંદુવત વિજભારથી $80\, cm$ અંતરે વિદ્યુતક્ષેત્રની પ્રબળતા કેટલી હશે?View Solution
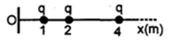
- 9View Solutionનીચે આપેલ આકૃતિમાં ઊગમબિંદુ આગળ અનંત સંખ્યાના વિદ્યુતભારને લીધે વિદ્યુતક્ષેત્રની ગણતરી કરો.
- 10$r_1$ અને $r_2$ ત્રિજ્યાની સમકેન્દ્રી રિંગ પર $Q_1$ અને $Q_2$ વિધુતભાર છે તો કેન્દ્રથી $r$ $(r_1 < r < r_2)$ અંતરે વિધુતક્ષેત્ર શોધોView Solution
