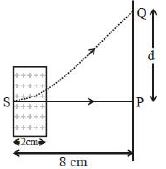
\({\text{R}} = \frac{{{\text{mv}}}}{{{\text{qB}}}}\)
\( = \frac{{\sqrt {2{\text{m}}({\text{KE}})} }}{{{\text{qB}}}}\)
\({\text{R}} = \frac{{\sqrt {2 \times 9.1 \times {{10}^{ - 31}} \times \left( {100 \times 1.6 \times {{10}^{ - 18}}} \right)} }}{{1.6 \times {{10}^{ - 10}} \times 1.5 \times {{10}^{ - 3}}}}\)
\({\text{R}} = 2.248\,{\text{cm}}\)
\(\sin \theta = \frac{2}{{2.248}};\,\,\,\,\,\tan \,\theta = \frac{{QU}}{{TU}}\)
\(\frac{2}{{1.026}} = \frac{{QU}}{6}\)
\(QU = 11.69\)
\({\text{PU}} = {\text{R}}(1 - \cos \,\theta )\)
\( = 1.22\)
\({\text{d}} = {\text{QU}} + {\text{PU}}\)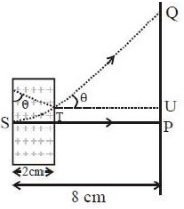
Download our appand get started for free
Similar Questions
- 1બે નાના વર્તુળાકાર ગૂચળા(એકપણ પાસે આત્મપ્રેરકત્વ નથી)માંથી એક ગૂચાળાને $V$ આકારના કોપરના તાર સાથે સમક્ષિતિજ સમતલ રહે તે રીતે લટકાવેલ છે. બીજા ગૂચળાને પહેલા ગૂચળાની નીચે સમક્ષિતિજ સમતલ રહે તે રીતે ગોઠવેલ છે. બંને ગૂચળાને $dc$ સ્ત્રોત સાથે શ્રેણીમાં જોડેલ છે. બંન્ને ગૂચળા એકબીજા તરફ આકર્ષણબળ લગાડે છે એવું જોવા મળતું હોય તો નીચે પૈકી કયું વિધાન ખોટું પડે?View Solution
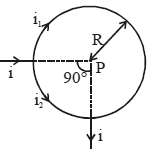
- 2એક $i$ પ્રવાહનું વહન કરતા વાહક તારને આકૃતિમાં દર્શાવ્યા પ્રમાણે બે ભાગમાં વિભાજિત કરેલ છે. તે વર્તુળાકાર લૂપની ત્રિજ્યા $R$ છે. તો કેન્દ્ર $P$ આગળ કુલ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 3આપેલ પરિપથ માટે $O $ બિંદુ પાસે ચુંબકીયક્ષેત્ર આપેલ છે તો નીચે પૈકી કયું સાચું થાય?View Solution
$(i)$ $(ii)$ $(iii)$ (A) $\frac{{{\mu _0}i}}{r}$ $\otimes$ (A) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\otimes$ (A) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{2r}}$ $\odot$ (B) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right)$ $\otimes$ (C) $\frac{{{\mu _0}i}}{{4r}}$ $\otimes$ (C) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\odot$ (C)$\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\odot$ (D) $\frac{{{\mu _0}i}}{{4r}}$ $\odot$ (D) $0$ (D) $0$ 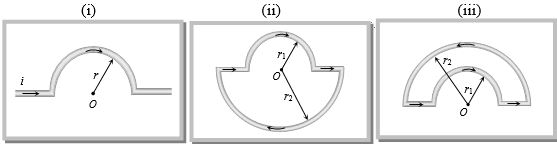
- 4નીચે બે વિધાનો આપ્યા છે :View Solution
વિધાન ($I$) : જ્યારે પ્રવાહ સમય સાથે બદલાતો હોય ત્યારે ન્યૂટનનો ત્રીજો નિયમ ત્યારે જ પ્રમાણિત થાય જયારે વિદ્યુતયુંબકીય ક્ષેત્ર દ્વારા લઈ જવાતું વેગમાન ધ્યાનમાં લેવામાં આવે.
વિધાન ($II$) : એમ્પિયરનો પરિપથીય નિયમ બાયો-સાવર્ટના નિયમ ઉપર આધાર રાખતો નથી.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિધાનોમાંથી સાચો ઉત્તર પસંદ કરો.
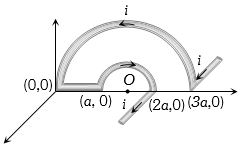
- 5આપેલ પરિપથમાં કેન્દ્ર $O$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 6$2000\,Ω$ નું વોલ્ટમીટર $2\,V$ માપી શકે છે.તેને $10\,V$ માપી શકે તેવું બનાવવા કેટલા ............ $\Omega $ અવરોધ શ્રેણીમાં જોડવો પડે?View Solution
- 7એક ઇલેકટ્રોન,એક પ્રોટ્રોન અને એક આલ્ફા કણની ગતિઊર્જા સમાન છે.તેઓ સમાન ચુંબકીયક્ષેત્ર $B$ માં અનુક્રમે $r_e,r_p$ અને ${r_\alpha }$ ત્રિજયા ધરાવતી વર્તુળાકાર કક્ષામાં ગતિ કરે છે. $r_e,r_p$ અને $\;{r_\alpha }$વચ્ચેનો સંબંધView Solution
- 8બંનેમાંથી સમાન પ્રવાહ પસાર થતો હોય તેવા બે ગૂંચળાઓ $X$ અને $Y$ ના કેન્દ્ર આગળ અનુક્રમે ચુંબકીય ક્ષેત્રો $B_X$ અને $B_Y$ છે. જે $X$ ગૂંચળામાં આંટાની સંખ્યા $200$ અને ત્રિજ્યા $20\,cm$ અને $Y$ ગુંચળામાં આંટાની સંખ્યા $400$ અને ત્રિજ્યા $20\,cm$ છે, તો $B_X$ અને $B_Y$ નો ગુણોતર થશે.View Solution
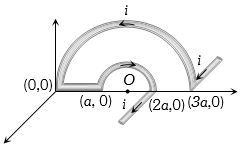
- 9આપેલ પરિપથમાં કેન્દ્ર $O$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 10રીંગની અક્ષ પર $0.05 \,m$ અને $0.2\, m$ અંતરે ચુંબકીયક્ષેત્રનો ગુણોત્તર $8:1$ હોય,તો રીંગની ત્રિજયા કેટલા ......$m $ હશે?View Solution
