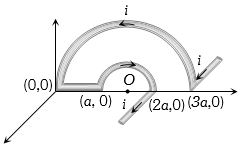
(b) Magnetic field at \(O\) due to Part \((1)\) : \({B_1} = 0\)
Part \((2)\): \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{(a/2)}} \otimes \)(along \(-Z-\)axis)
Part \((3)\): \({B_3} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{{(a/2)}}\left( \downarrow \right)\)(along \(-Y-\)axis)
Part \((4)\): \({B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{{(3a/2)}}\odot\)(along \(+Z-\)axis)
Part \((5)\): \({B_5} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{{(3a/2)}}\left( \downarrow \right)\)(along -\(Y\) \(-\) axis) \({B_2} - {B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{a}\left( {2 - \frac{2}{3}} \right) = \frac{{{\mu _0}i}}{{3a}} \otimes \)(along -\(Z\) \(-\) axis) \({B_3} + {B_5} = \frac{{{\mu _0}}}{{4\pi }}.\frac{1}{a}\left( {2 + \frac{2}{3}} \right) = \frac{{8{\mu _0}i}}{{12\pi a}}\left( \downarrow \right)\) (along -\(Y\)\( -\) axis)
Hence net magnetic field \({B_{net}} = \sqrt {{{({B_2} - {B_4})}^2} + {{({B_3} + {B_5})}^2}} \)\( = \frac{{{\mu _0}i}}{{3\pi a}}\sqrt {{\pi ^2} + 4} \)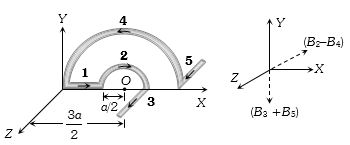
Download our appand get started for free
Similar Questions
- 1તારમાંથી $5\,A$ નો પ્રવાહ પસાર થાય છે,તારથી $0.1\,m$ અંતરે $ 5 \times {10^6}m{s^{ - 1}} $ ના વેગથી ઇલેકટ્રોન તારને સમાંતર ગતિ કરે,તો તેના પર કેટલું બળ લાગતું હશે?View Solution
- 2એક વિસ્તારમાં એકબીજાને લંબરૂપે $20\; Vm ^{-1}$ જેટલું વિદ્યુતક્ષેત્ર અને $0.5\;T$ ચુંબકીયક્ષેત્ર બંને પ્રવર્તે છે. તેમાં એક ઇલેકટ્રોન બંનેને લંબરૂપે અચળ વેગથી ગતિ કરતો હોય, તો તેનો વેગ કેટલો હશે?View Solution
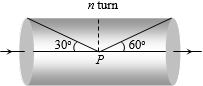
- 3આપેલ આકૃતિમાં $P $ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 4$q$ વિજભાર અને $m$ દળ ધરાવતો કણ $+ x$ અક્ષની દિશામાં વહે છે. $\Delta t$ સમય સુધી $B$ ચુંબકીયક્ષેત્ર એવી રીતે લગાવવામાં આવે કે જેથી કણ $y$ અક્ષ પર $d$ અંતરે હોય ત્યારે પોતાની દિશા ઉલટાવે છે.View Solution
- 5$30$ કાપા ધરાવતા ગેલ્વેનોમીટરની વિધુતપ્રવાહ સંવેદીતા $20$ $\mu A$ કાપા. ક્રમની છે. તેનો અવરોધ $25\,\Omega$ નો છે. આ એમિટરને $1$ વોલ્ટના વોલ્ટમીટર કેવી રીતે ફેરવશો ............. $\Omega$View Solution
- 6View Solutionવિદ્યુત પ્રવાહધારીત ગૂચાળાને ચુંબકીયક્ષેત્રમાં મૂકવામાં આવે છે. તેનું ભ્રમણ એવી રીતે થાય કે જેથી તેનું સમતલ ............
- 7$R$ ત્રિજયા ધરાવતી રીંગ પરના $A$ અને $B$ બિંદુ વચ્ચે બેટરી લગાવેલ છે. $AB$ એ કેન્દ્ર આગળ $ \theta $ ખૂણો બનાવે છે.તો કેન્દ્ર પર ચુંબકીયક્ષેત્ર...View Solution
- 8View Solutionકોઇલનો ટોર્ક વિરુધ્ધ ખૂણાનો ગ્રાફ નીચે પૈકી કયો છે?
- 9અચળ વેગ સાથે ગતિ કરતો પ્રોટોન અવકાશના વિસ્તારમાંથી તેના વેગમાં ફેરફાર થયા વગર, પસાર થાય છે. જો $E$ અને $B$ નીચેનામાંથી ક્યું હોઈ શકે ?View Solution
- 10$30$ કાપા ધરાવતા ગેલ્વેનોમીટરની વિધુતપ્રવાહ સંવેદીતા $20\,\mu A$ કાપા. ક્રમની છે. તેનો અવરોધ $25\, \Omega$ નો છે.$1$ એમ્પિયર પ્રવાહ માપવા માટે, તમે તેને કેવી રીતે એમિટરમાં ફેરવશો.View Solution
