આકૃતિમાં કેપેસીટરનો પરિપથ આપેલ છે જેમાં બધા કેપેસીટરના મૂલ્યો માઇક્રોફેરાડે માં છે જો $A$ અને $B$ વચ્ચેનો સમતુલ્ય કેપેસીટન્સ $1\,\mu F$ હોય તો $C$ નું મૂલ્ય કેટલું હશે?
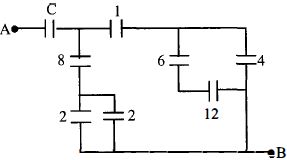

JEE MAIN 2016, Diffcult
a
Capacitors \(2\, \mu \mathrm{F}\) and \(2\, \mu \mathrm{F}\) are parallel, their equivalent \(=4\, \mu \mathrm{F}\)
Capacitors \(2\, \mu \mathrm{F}\) and \(2\, \mu \mathrm{F}\) are parallel, their equivalent \(=4\, \mu \mathrm{F}\)
\(6 \,\mu \mathrm{F}\) and \(12\, \mu \mathrm{F}\) are in series, their equivalent \(=4\, \mu \mathrm{F}\)
Now \(4 \,\mu F(2 \text { and } 2\, \mu F)\) and \(8\, \mu F\) in series
\(=\frac{3}{8}\, \mu F\)
And \(4\, \mu \mathrm{F}(12 \& 6\, \mu \mathrm{F})\) and \(4\, \mu \mathrm{F}\) in parallel \(=4+4=8\, \mu \mathrm{F}\)
\(8\, \mu \mathrm{F}\) in series with \(1\, \mu \mathrm{F}=\frac{1}{8}+1 \Rightarrow \frac{8}{9}\, \mu \mathrm{F}\)
Now \(C_{e q}=\frac{8}{9}+\frac{8}{3}=\frac{32}{9}\)
\(C_{eq}\) of circuit \(=\frac{32}{9}\)
With \(C-\frac{1}{C_{e q}}=\frac{1}{C}+\frac{9}{32}=1 \Rightarrow C=\frac{32}{23}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$R$ અને $2 R$ ત્રિજ્યા ધરાવતા બે ધાતુના ગોળાની પૃષ્ઠવિજભાર ઘનતા $\sigma$ સમાન છે.તે બંનેને સંપર્કમાં લાવવામાં આવે છે અને પછી અલગ કરવામાં આવે છે.તો તેના પર નવી પૃષ્ઠવિજભાર ઘનતા કેટલી થશે?View Solution
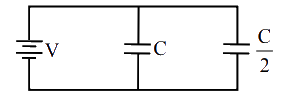
- 2આકૃતિમાં દર્શાવ્યા મુજબ કેપેસિટર $C$ અને $\frac{C}{2}$ ને બેટરી સાથે જોડેલા છે.આ બંને કેપેસિટરને સંપૂર્ણ ચાર્જ કરવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 3$R$ ત્રિજ્યાની ધાત્વિય ગોળીય કવચના કેન્દ્રથી ત્રિજ્યાવર્તી અંતર $r$ નો વિધુતસ્થિતિમાન સાથેનો આલેખ નીચેનામાંથી ક્યો છે?View Solution
- 4$20\, cm$ અને $15\, cm$ ત્રિજ્યાવાળા વાહકગોળા અહાવક સ્ટેનડ પર મૂકેલા છે. બંને ઉપર સમાન $10\ \mu C $ જેટલો વિદ્યતભાર છે. તેઓને તાંબાના તાર સાથે જોડીને અલગ કરતાં .....View Solution
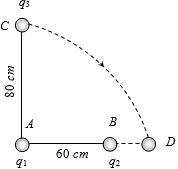
- 5$q_1 = + 2 \times 10^{-8}\ C$ અને $q_2 = -0.4 \times 10^{-8}\ C$ છે, $q_3 = 0.2 \times 10^{-8}\ C$ વિદ્યુતભારને $C$ થી $D$ લઇ જવાથી $q_3$ ની સ્થિતિઊર્જામાં...View Solution
- 6$2 \;F$ સંધારકતા ધરાવતા એક સમાંતર પ્લેટ સંધારકને $V$ સ્થિતિમાન સુધી વિદ્યુતભારિત કરવામાં આવે છે. સંધારકમાં સંગ્રહિત ઊર્જા $E_1$ છે. આ સંધારક બીજા સમાન અવિદ્યુતભારિત સંધારક સાથે સમાંતરમાં જોડવામાં આવે છે. આ સંયોજનમાં સંગ્રહિત ઊર્જા $E_2$ છે. ગુણોત્તર $E _2 / E _1$ ........ થશે.View Solution
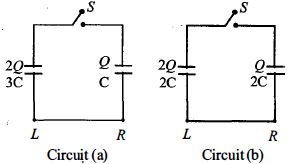
- 7બે પરિપથ $(a)$ અને $(b)$ પર $C, 2C$ અને $3C$ કેપેસીટન્સ ધરાવતા કેપેસીટર પર વિજભાર છે.દરેક કેપેસીટર પરનો વિજભાર આકૃતિમાં દર્શાવેલ છે.જો કળ બંધ કરવામાં આવે તો..View Solution
- 8$A$ ક્ષેત્રફળ અને બે પ્લેટો વચ્ચેનું અંતર $d$ ધરાવતા સમાંતર પ્લેટ કેપેસિટર આપેલ છે તેમાં સમાન ક્ષેત્રફળ ધરાવતા અને $\frac{d}{2}$ જેટલી જાડાઈ અને ડાઈ ઇલેક્ટ્રીક અચળાંક $K = 4$ ધરાવતો સ્લેબ દાખલ કરતાં મળતા નવા કેપેસિટન્સ અને જૂના કેપેસિટન્સનો ગુણોત્તર શોધો.View Solution
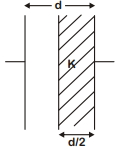
- 9કેપેસિટરને $100\, V$ ચાર્જ કરવામાં આવે છે.તેમાં $2\,mm$ ડાઇઇલેકિટ્રક પ્લેટ નાખતાં પહેલા જેટલો વોલ્ટેજ કરવા માટે બે પ્લેટ વચ્ચેનું અંતર $1.6\,mm$ વધારવું પડે છે.તો ડાઇઇલેકિટ્રકનો ડાઇઇલેકિટ્રક અચળાંક કેટલો હશે?View Solution
- 10View Solutionનીચેનામાંથી કઈ આકૃતિ બે ધન વિદ્યુતભારના તંત્રની યોગ્ય સમસ્થિતિમાન સપાટી દર્શાવે છે?
