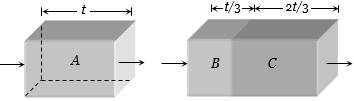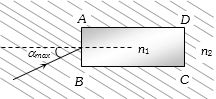
(a) Ray comes out from \(CD,\) means rays after refraction from \(AB\) get, total internally reflected at \(AD\)
\(\frac{{{n_1}}}{{{n_2}}} = \frac{{\sin {\alpha _{\max }}}}{{\sin {r_1}}} \Rightarrow {\alpha _{\max }} = {\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\sin {r_1}} \right]\) …\((i) \)
Also \({r_1} + {r_2} = {90^o} \Rightarrow {r_1} = 90 - {r_2} = 90 - C\)
\( \Rightarrow \)\({r_1} = 90 - {\sin ^{ - 1}}\left({\frac{1}{{_2{\mu _1}}}} \right) \Rightarrow {r_1} = 90 - {\sin ^{ - 1}}\left({\frac{{{n_2}}}{{{n_1}}}} \right)\) ...\((ii)\)
Hence from equation \((i)\) and \((ii)\)
\({\alpha _{\max }} = {\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\sin \left\{ {90 - {{\sin }^{ - 1}}\frac{{{n_2}}}{{{n_1}}}} \right\}} \right]\)
= \({\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left({{{\sin }^{ - 1}}\frac{{{n_2}}}{{{n_1}}}} \right)} \right]\)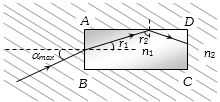
Download our appand get started for free
Similar Questions
- 1ખાલી બીકરમાં સિકકો પડેલ છે,તે માઇક્રોસ્કોપ દ્વારા ફોકસ કરેલ છે,તેમાં $10 \,cm$ ઊંચાઇ સુધી પાણી ભરતાં તેને ફરીથી ફોકસ કરવા માટે માઇક્રોસ્કોપને કેટલું ખસેડવું પડે?View Solution
- 2પ્રકાશનું એક અભિસારિત કિરણ એ અપસારી લેન્સ પર પડે છે. લેન્સમાંથી પસાર થયા પછી, પ્રકાશના કિરણો લેન્સની બીજી બાજુએ $15 \,cm$ ના અંતરે એકબીજાને છેદે છે. જો લેન્સ દૂર કરવામાં આવે, તો કિરણોના છેદન બિંદુ લેન્સથી $5\,cm$ નજીક તરફ ખસે છે. લેન્સની કેન્દ્રલંબાઇ ($cm$ માં) કેટલી હશે?View Solution
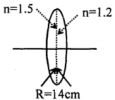
- 3દ્વિ બહિર્ગોળ લેન્સ બે પાતળા સમતલીય બહિર્ગોળ લેન્સથી બનાવેલો છે. પહેલાં લેન્સનો વક્રીભવનાંક $1.5 $અને બીજાનો $1.2$ છે. બંન્ને વક્ર સપાટીની વક્રતાત્રિજ્યા $ R\, 14 \,cm$ છે. આ દ્વિ બહિર્ગોળ લેન્સથી $40\, cm$ દૂર પદાર્થ મૂક્લો છે. તેનું પ્રતિબિંબ કેટલા .....$cm$ મળશે?View Solution
- 4એક સમઘન રૂમ અરીસાથી બનાવેલ છે.તળિયાના વિકર્ણ પર એક કીડી ગતિ કરે છે. ત્યારે બે અડકેલી દિવાલના અરીસામાં પ્રતિબિંબનો વેગ $10 cms^{-1}$ હોય,તો છતના અરીસામાં પ્રતિબિંબનો વેગ કેટલો થાય?View Solution
- 5વિધાન $- 1$ : ખૂબ મોટા પરિમાણ ધરાવતો ટેલિસ્કોપ વક્રીભવન ટેલેસ્કોપને બદલે પરાવર્તન ટેલેસ્કોપ હોયView Solution
વિધાન $- 2$ : મોટા પરિમાણના અરીસા માટે યાંત્રિક આધાર આપવો, મોટા લેન્સને આપવા પડતાં આધાર કરતાં સહેલો પડે
- 6$1.5$ વક્રીભવનાંકના ઘટ્ટ માધ્યમની અંતર્ગોળ સપાટીની વક્રતાત્રિજ્યા $12\, cm$ છે. ઘટ્ટ માધ્યમની ધ્રુવથી $9 \,cm$ અંતરે એક વસ્તુ રહેલી છે. હવામાં વક્રીભવનના કારણે પ્રતિબિંબનું સ્થાન શોધો.View Solution
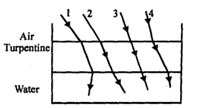
- 7View Solutionટર્પેંનટાઈનની પ્રકાશીય ઘનતા પાણી કરતાં વધારે હોય છે. જ્યારે ની દળ ઘનતા ઓછી હોય છે. આકૃતિ પાત્રમાં પાણી ઉપર તરતું ટર્પેંનટ્ઈનનું સ્તર દર્શાવે છે. જેના માટે આકૃતિ મુજબ ટર્પેંનટાઈન પર ચારમાંથી એક કિરણ આપાત થાય છે. તો તે કિરણ સાચો પથ દર્શાવો.
- 8View Solutionઆકૃતિ મુજબના લેન્સ દ્વારા.....

- 9પ્રકાશનું કિરણ $\alpha $ ખૂણે ગાળીય કાચ પર આપાત થઇને $\beta $ ખૂણે વક્રીભૂત થાય છે.તો નિર્ગમન કિરણ આપાતકિરણ સાથે કેટલો ખૂણો બનાવે?View Solution
- 10$A$ અને $C $ નો વક્રીભવનાંક $1.5 $ અને $1.6 $ છે. $B$ અને $C$ ની જાડાઇનો ગુણોત્તર $1:2$ છે.બંને પર કિરણ આપાત કરતાં બંને બ્લોકમાં તરંગોની સંખ્યા સમાન હોય, તો $B$ નો વક્રીભવનાંક કેટલો હશે?View Solution