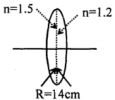
દ્વિ બહિર્ગોળ લેન્સ બે પાતળા સમતલીય બહિર્ગોળ લેન્સથી બનાવેલો છે. પહેલાં લેન્સનો વક્રીભવનાંક $1.5 $અને બીજાનો $1.2$ છે. બંન્ને વક્ર સપાટીની વક્રતાત્રિજ્યા $ R\, 14 \,cm$ છે. આ દ્વિ બહિર્ગોળ લેન્સથી $40\, cm$ દૂર પદાર્થ મૂક્લો છે. તેનું પ્રતિબિંબ કેટલા .....$cm$ મળશે?

Diffcult
b
\(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
\(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
For the first lens,
\(n=1.5, R_{1}=+14 cm , R_{2}=\infty\)
\(\therefore \frac{1}{f_{1}}=(1.5-1)\left(\frac{1}{14}-\frac{1}{\infty}\right)\)
\(=\frac{0.5}{14}\)
For the second lens,
\(n=1.2, R_{1}=\infty, R_{2}=-14 cm\)
\(\therefore \frac{1}{f_{1}}=(1.2-1)\left(\frac{1}{\infty}-\frac{1}{-14}\right)=\frac{0.2}{14}\)
The focal length of the bi-convex lens is
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
\(=\frac{0.5}{14}+\frac{0.2}{14}=\frac{0.7}{14}=\frac{1}{20}\)
According to thin lens formula,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
Here, \(u=-40 cm , f=20 cm\)
\(\therefore \frac{1}{v}-\frac{1}{-40}=\frac{1}{20}\) or
\(\frac{1}{v}=\frac{1}{20}-\frac{1}{40}\) or
\(v=40 cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પ્રકાશનું કિરણ માધ્યમમાંથી હવામાં પ્રવેઢે છે જે બે ખૂણે આપાત થાય છે $(A)\, 20^o$ અને $(B)\, 40^o$ .જો તે માધ્યમમાં $0.2\, ns$ માં $3.0\, cm$ ગતિ કરતું હોય તો કિરણ .....View Solution
- 2$f / 3$ લંબાઈનો પાતળો સળિયો $f $ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાની મુખ્ય અક્ષ પર એવી રીતે મૂક્યો છે કે જેથી તેનું પ્રતિબિંબ વાસ્તવિક અને જે સળિયામાં માત્ર સ્પર્શતું છે, તો મોટવણીનું મૂલ્ય..... હશે.View Solution
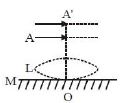
- 3પાતળા લેન્સ $L$ (વક્રીભવનાંક $=1.5$) ને સમતલ અરીસા $M$ પર મુકેલ છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે $OA = 18\, cm$ થાય તે રીતે એક પિનને $A$ પર મુક્તા તેનું વાસ્તવિક અને ઊલટું પ્રતિબિંબ $A$ પર જ મળે છે.જ્યારે લેન્સ અને અરીસા વચ્ચે ${\mu _1}$ વક્રીભવનાંક ધરાવતું પ્રવાહી મુક્તા પિનને $OA’ = 27\,cm$ થાય તે રીતે $A'$ પર ખસેડતા તેનું વાસ્તવિક અને ઊલટું પ્રતિબિંબ પ્રતિબિંબ $A’$ આગળ જ મળે છે તો $\mu_1$ નું મૂલ્ય કેટલું હશે?View Solution
- 4$f=5 \,cm$ કેન્દ્રલંબાઈના સાદા સૂક્ષ્મદર્શક વડે રચાતી મહત્તમ મોટવણી કેટલી છે ?View Solution
- 5પ્રિઝમમાંથી પીળો પ્રકાશ લઘુતમ વિચલન સાથે વક્રીભૂત થાય છે. જો $i_1$ અને $i_2$ પ્રિઝમ માટે આપાતકોણ અને નિર્ગમનકોણ હોય, તોView Solution
- 6સાદા ટેલિસ્કોપમાં ઓબ્જિેકિટવપીસની કેન્દ્રલંબાઇ $100cm$ અને આઇપીસની કેન્દ્રલંબાઇ $2 cm$ છે. વસ્તુમાંથી આવતા કિરણો આંખ પાસે $0.5^o$ નો ખૂણો બનાવે છે.હવે વસ્તુને ટેલિસ્કોપમાં જોવાથી વસ્તુનું પ્રતિબિંબ આંખ પાસે કેટલા .......$^o$ ખૂણો બનાવે?View Solution
- 7બિંદુવત વસ્તુ સમતલ બહિર્ગોળ લેન્સની સામે પડેલ છે.લેન્સની વક્ર સપાટીની ત્રિજ્યા $30 \;\mathrm{cm}$ અને વક્રીભવનાંક $1.5$ છે તો લેન્સની કેન્દ્રલંબાઈ ($\mathrm{cm}$ માં) કેટલી થશે?View Solution
- 8$\sqrt 3 $ વક્રીભવનાંકના કાચના લંબચોરસ સ્લેબમાં પ્રકાશનું કિરણ $60° $ આપાત કોણે પ્રવેશે છે. તે સ્લેબમાં $5 \,cm $ અંતર કાપીને સ્લેબની બહાર નિર્ગમન પામે છે. આપાત અને નિર્ગમન કિરણ વચ્ચેનું લંબ અંતર શું થશે?View Solution
- 9એક વ્યક્તિનું નજીકબિંદુ $75 \,cm$ છે. તે $30\, cm$ અંતરે રહેલું પુસ્તક વાંચી શકે તે માટે ચશ્માના લેન્સનો પાવર કેટલો હોવો જોઈએ.View Solution
- 10$160\,cm$ ઊંચાઈ ધરાવતો માણસ સમતલ અરીસાની સામે ઊભા છે. તેની આંખ જમીન થી $150\,cm$ ઊંચાઈએ છે. માણસને પોતાનું પ્રતિબિંબ આખું જોવા માટે અરીસાની લઘુતમ લંબાઈView Solution
