આપેલ આકૃતિમાં $P$ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?
Diffcult
Download our app for free and get started
d
\(B = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}(\sin {\varphi _1} + \sin {\varphi _2})\),
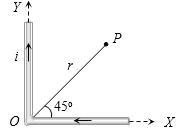
\(B = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}(\sin {\varphi _1} + \sin {\varphi _2})\),
\(d = r\sin {45^o} = \frac{r}{{\sqrt 2 }}\)
\(B = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{{(r/\sqrt 2 )}}(\sin {45^o} + \sin {90^o})\)
\( = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}(\sqrt 2 + 1)\)
\({B_{net}} = 2 \times \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}(\sqrt 2 + 1) = \frac{{{\mu _0}}}{{2\pi }}.\frac{i}{r}(\sqrt 2 + 1)\)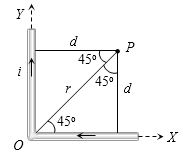
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિધાન $- 1$ : એક વિજભારિત કણ સ્થિત ચુંબકીયક્ષેત્રને લંબ ગતિ કરે છે. આ ગતિ દરિમિયાન વિજભારિત કણની ગતિઉર્જા બદલાતી નથી.View Solution
વિધાન $- 2$ : સ્થિત ચુંબકીયક્ષેત્ર ગતિ કરતાં વિજભારિત કણ પર ચુંબકીયક્ષેત્રને લંબ દિશામાં બળ લગાવે છે.
- 2$12\, A$ પ્રવાહધારીત તારથી કેટલા અંતરે ચુંબકીયક્ષેત્ર $3 \times 10^{-5} Wb / m ^{2}$ થાય?View Solution
- 3બે સમાંતર તારોમાંથી પસાર થતાં પ્રવાહ $10\,A$ અને $2\,A$ વિરુધ્ધ દિશામાં છે,એક તાર અનંત લંબાઇનો અને બીજો તાર $2\,m$ લંબાઇનો છે.બંને તાર વચ્ચેનું અંતર $10\,cm$ છે.તો $2\,m$ ના તાર પર કેટલું બળ લાગે?View Solution
- 4$10\; cm$ બાજુ વાળા એક ચોરસ ગૂંચળાને $20$ આંટા છે અને તેમાંથી $12\; A$ વિદ્યુતપ્રવાહ પસાર થાય છે. આ ગૂંચળુ શિરોલંબ લટકાવેલું છે અને ગૂંચળાના સમતલનો લંબ $0.80 \;T$ મૂલ્યના સમક્ષિતિજ નિયમિત ચુંબકીય ક્ષેત્ર સાથે $30^o$ કોણ બનાવે છે. ગૂંચળું કેટલા મૂલ્યનું ટૉર્ક અનુભવશે?View Solution
- 5એક પ્રોટોન અને એક આલ્ફા કણ, સમાન ચુંબકીય ક્ષેત્ર $B$ માં તેને લંબરૂપે ગતિ કરતાં પ્રવેશ કરે છે. જો બંને કણો માટે, વર્તુળાકાર કક્ષા માટેની ત્રિજયા સમાન હોય અને પ્રોટોન દ્વારા મેળવાતી ગતિઊર્જા $ 1 \,MeV$ હોય, તો આલ્ફા કણ દ્વારા મેળવાતી ગતિઊર્જા $MeV$ માં કેટલી હશે?View Solution
- 6વર્તુળાકાર આડછેદ અને સ્થિત વિદ્યુતપ્રવાહ ઘરાવતા લાંબા સીધા તાર માટના એમ્પિયર પરિપથીય નિયમ $(circuital\, law)$ થી તારના અંદરના અને બહારના વિસ્તારમાં ચુંબકીય ક્ષેત્રનો ફેરફાર$.....$View Solution
- 7$0.3\; T$ નું એકસમાન ચુંબકીયક્ષેત્ર ધન $Z - $ દિશામાં પ્રસ્થાપિત કરેલ છે. $XY$ સમતલમાં $10\; cm $ અને $5\; cm$ બાજુઓવાળી એક $I=12\; A$ પ્રવાહધારીત લંબચોરસ લૂપને આકૃતિમાં દર્શાવ્યા મુજબ મૂકેલ છે. આ લૂપ પરનું ટોર્ક કેટલું થાય?View Solution
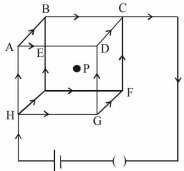
- 8આકૃતિ મુજબ $d$ જેટલી સમાન લંબાઈ એ સમાન અવરોધ ધરાવતા વાયરોથી એક ધન બનાવવામાં આવેલ છે અને તેમાં સ્થિર પ્રવાહ પસાર થાય છે. આ રચનાના કારણે તેના કેન્દ્ર $p$ માં ચુંબકીય ક્ષેત્ર શું હશે?View Solution
- 9નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ :બાયો-સાર્વટનો નિયમ પ્રવાહ ધરાવતા સુવાહકના ફક્ત અતિસુક્ષ્મ વિદ્યુતખંડ $(Idl)$ ને કારણે ઉત્પન્ન ચુંબકીય ક્ષેત્રની તીવ્રતાનું સૂત્ર આપે છે.
વિધાન $II$ :બાયો-સાર્વટનો નિયમ વીજભાર $q$ માટે કુલંબના પ્રતિવર્ગના નિયમ જેવો જ છે, કે તેમાં પ્રથમ એ અદિશ ઉદગમ $Idl$ ને કારણે ઉત્પન્ન ક્ષેત્ર સાથે સંકળાયેલ છે જ્યારે પછીનો એ સદિશ ઉદગમ $q$ ને કારણે ઉત્પન્ન ક્ષેત્ર સાથે સંકળાયેલ છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય વિક્લ્પ પસંદ કરો.
- 10એક ચલિત ગૂંચળાવાળા ગેલ્વેનોમીટરમાં પ્રવાહ સંવેદિતા. $50 \%$ વધારવા માટે ગૂંચળામાં આંટાની સંખ્યા વધારવામાં આવે છે. ગેલ્વેનોમીટરની વોલ્ટેજ સંવેદિતામાં $..........\%$ પ્રતિશત ફેરફાર થશે.View Solution