The kinetic energy acquired by a charged particle in a uniform magnetic field \(B\) is
\(K=\frac{q^{2} B^{2} R^{2}}{2 m}\left(\text { as } R=\frac{m v}{q B}=\frac{\sqrt{2 m K}}{q B}\right)\)
where \(q\) and \(m\) are the charge and mass of the partic and \(R\) is the radius of circular orbit
\(\therefore \) The kinetic energy acquired by proton is
\(K_{p}=\frac{q_{p}^{2} B^{2} R_{p}^{2}}{2 m_{p}}\)
and that by the alpha particle is
\(K_{\alpha}=\frac{q_{\alpha}^{2} B^{2} R_{\alpha}^{2}}{2 m_{\alpha}}\)
Thus, \(\frac{K_{\alpha}}{K_{p}}=\left(\frac{q_{\alpha}}{q_{p}}\right)^{2}\left(\frac{m_{p}}{m_{\alpha}}\right)\left(\frac{R_{\alpha}}{R_{p}}\right)^{2}\)
or \(\quad K_{\alpha}=K_{p}\left(\frac{q_{\alpha}}{q_{p}}\right)^{2}\left(\frac{m_{p}}{m_{\alpha}}\right)\left(\frac{R_{\alpha}}{R_{p}}\right)^{2}\)
Here, \(K_{p}=1\) \(MeV\) \(, \frac{q_{\alpha}}{q_{p}}=2, \frac{m_{p}}{m_{\alpha}}=\frac{1}{4}\)
and \(\frac{R_{\alpha}}{R_{p}}=1\)
\(\therefore \quad K_{\alpha}=(1\, \mathrm{MeV})(2)^{2}\left(\frac{1}{4}\right)(1)^{2}=1 \,\mathrm{MeV}\)
Download our appand get started for free
Similar Questions
- 1$80 \,cm$ લંબાઈના એક સોલેનોઈડ પર પાસ-પાસે દરેક $400$ આંટા વાળા $5$ આવરણ વિંટાળ્યા છે. સોલેનોઈડનો વ્યાસ $1.8 \,cm$ છે. જો સોલેનોઈડમાં $8.0 \,A$ વિદ્યુતપ્રવાહ વહેતો હોય, તો તેના કેન્દ્ર પાસે $B$ નું મૂલ્ય શોધો.View Solution
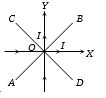
- 2બે અત્યંત પાતળા ધાતુના સમાન પ્રવાહ ધરાવતા તારને $X$ અને $Y$ અક્ષ પર દર્શાવ્યા પ્રમાણે મૂકેલા છે. $AB$ અને $CD$ રેખાઓ મૂળ અક્ષ સાથે $45^\circ $ પર અને ઉગમબિંદુ $O$ માંથી પસાર થાય છે. કઈ રેખા પર ચુંબકીયક્ષેત્ર શૂન્ય હશે?View Solution
- 3View Solutionજો સ્પિંગમાંથી વિદ્યુતપ્રવાહ પસાર કરવામાં આવે, તો તે
- 4નીચે બે વિધાનો આપ્યા છે :View Solution
વિધાન ($I$) : જ્યારે પ્રવાહ સમય સાથે બદલાતો હોય ત્યારે ન્યૂટનનો ત્રીજો નિયમ ત્યારે જ પ્રમાણિત થાય જયારે વિદ્યુતયુંબકીય ક્ષેત્ર દ્વારા લઈ જવાતું વેગમાન ધ્યાનમાં લેવામાં આવે.
વિધાન ($II$) : એમ્પિયરનો પરિપથીય નિયમ બાયો-સાવર્ટના નિયમ ઉપર આધાર રાખતો નથી.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિધાનોમાંથી સાચો ઉત્તર પસંદ કરો.
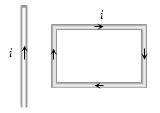
- 5View Solutionચોરસ ફ્રેમ કઇ બાજુ ગતિ કરશે?
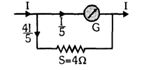
- 6કોઈ ચલિત ગુંચળું ધરાવતા ગેલ્વેનોમીટરનો અવરોધ $50\,ohm,$ અને તેના પર $25$ કાપા છે. જ્યારે તેમાંથી $4\times 10^{-4}$ એમ્પિયર પ્રવાહ પસાર થાય ત્યારે તેની સોય (દર્શક) એક કાપા જેટલું આવર્તન અનુભવે છે. આ ગેલ્વેનોમીટરને $2.5\,V$ ના વોલ્ટમીટર તરીકે વાપરવું હોય તો તેને ____________$ohm$ અવરોધ સાથે જોડવું પડશેView Solution
- 7એક વિઘુતભાર $q$ એક વિસ્તારમાં ગતિ કરે છે જ્યાં સમાન વિદ્યુતક્ષેત્ર અને સમાન ચુંબકીયક્ષેત્ર પ્રવર્તે છે, તો તેના પર લાગતું બળ કેટલું હશે?View Solution
- 8$5\,cm$ ત્રિજ્યા ધરાવતા અને એકદદમ નજીક-નજીક વીંટળાયેલા વર્તુળાકાર ગૂંચળા (ગાળા) ને કારણે તેના કેન્દ્ર આગળ $37.68 \times 10^{-4}\,T$ જેટલું ચુંબકીયક્ષેત્ર ઉત્પન્ન થાય છે. ગૂંચળાંમાંથી વહેતો પ્રવાહ $..........\;A$ છે. [ધારો કે આંટાની સંખ્યા $100$ છે અને $\pi=3.14$ ]View Solution
- 9આયનિય હાઈડ્રોજન પરમાણુઓ અને $\alpha -$કણો સમાન વેગમાનથી અચળ ચુંબકીય ક્ષેત્ર $B$ માં લંબ રીતે પ્રવેશે છે. તેમના પથોની ત્રિજ્યાઓનો ગુણોત્તર ${r_H}:{r_\alpha }$ કેટલો હશે?View Solution
- 10જ્યારે $4\,\Omega$ ના શંટને ગેલ્વેનોમીટર સાથે જોડવામાં આવે તો વિચલન $1/5$ જેટલું ઘટે છે. જો વધારાનો $2\,\Omega$ નો શંટ જોડવામાં આવે તો વિચલન કેટલું હશે ?View Solution