આપેલ અર્ધકોષ પ્રક્રિયા માટે $pH = 5$ પર વિધુતધ્રુવ પોટેન્શિયલ શું થશે ?
$2 \mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{O}_{2}+4 \mathrm{H}^{\oplus}+4 \mathrm{e}^{-} ; \mathrm{E}_{\mathrm{red}}^{0}=1.23 \mathrm{V}$ અને $ - 5 \times {10^{ - 4}}\,V\,{K^{ - 1}}$ છે. કોષપ્રક્રિયા $(\mathrm{R}=8.314 \;\mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1} ; \text { Temperature }=298 \;\mathrm{K} ;$ ઓક્સિજન એ પ્રમાણિત વાતાવરણ દબાણ $1$ બાર હેઠળ છે)
JEE MAIN 2020, Diffcult
Download our app for free and get started
a
\(\mathrm{O}_{2}(\mathrm{g})+4 \mathrm{H}^{+}+4 \mathrm{e}^{-} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(l) ; \mathrm{E}_{\mathrm{red.}}^{0}=1.23 \mathrm{V}\)
From nernst equation
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{0}-\frac{\mathrm{RT}}{\mathrm{nF}} \ln \mathrm{Q}\)
at \(1\; bar\) and \(298 \mathrm{K}\)
\(\frac{2.303 \mathrm{RT}}{\mathrm{F}}=0.059\)
\(\mathrm{pH}=5 \Rightarrow\left[\mathrm{H}^{+}\right]=10^{-5} \mathrm{M}\)
\(\mathrm{E}_{\text {cell }}=1.23-\frac{0.059}{4} \log \left[\mathrm{H}^{+}\right]^{4}\)
\(\mathrm{E}_{\text {cell }}=1.23-\frac{0.059}{4} \log \left(10^{-5}\right)^{4}\)
\(=1.23+0.295=1.525 \mathrm{V}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અહી આપેલ $E_{{K^ + }/K}^o\, = \, - \,2.93\,V\,;$View Solution
$E_{F{e^{2 + }}/Fe}^o\, = \, - \,0.44\,\,V\,;\,\,E_{Z{n^{2 + }}/Zn}^o\, = \, - \,0.76\,\,V\,;\,$
$E_{C{u^{ + 2}}/Cu}^o\, = \,0.34\,\,V$
આ ડેટાના આધારે, નીચેનામાંથી સૌથી વધુ રિદ્ક્ષન કર્તા ઘટક કયું છે?
- 2View Solutionપાણીમાં સોડીયમ સલ્ફેટનું દ્રાવણ એ પ્લેટીનમ ધ્રુવ વાપરીને વિદ્યુતવિભાજન કરવામાં આવે છે. કેથોડ અને એનોડ ઉપરની નીપજો અનુક્રમે કઈ છે?
- 3એ $0.5\,M\,NaOH$ દ્રાવણ ઓરડાના તાપમાને વાહકતા કોષમાં$31.6\,ohm$ નો પ્રતિકાર પ્રદાન કરે છે.જો કોષનો કોષ સતત $0.367\,cm^{-1}$ હોય તો આ $NaOH$ દ્રાવણ ની આશરે મોલર વાહકતા શું હશે?View Solution
- 4View Solutionપ્રમાણિત હાઈડ્રોજન વિદ્યુતધ્રુવનો વિદ્યુતધ્રુવ પોટેન્શિયલ શૂન્ય થાય છે કારણ કે
- 5કોષને ધ્યાનમાં લો:View Solution
$Pt ( s )\left| H _2( s )( latm )\right| H ^{+}\left( aq ,\left[ H ^{+}\right]=1\right)|| Fe ^{3+}( aq ), Fe ^{2+}( aq ) \mid \operatorname{Pt}( s )$
આપેલ : $E _{ Fe ^{3+} / e ^{2 *}}^0=0.771\,V$ અને $E _{ H ^{+}+\frac{1}{2} H _2}^0=0\,V , T =298\,K$
જો કોષનો પોટેન્શિયલ $0.712\,V$, હોય, તો $Fe ^{-2}$ થી $Fe ^{+3}$ ની સાંદ્રતાની ગુણોત્તર છે.(નજીકનો પૂર્ણાંક)
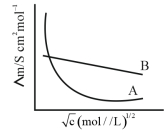
- 6સાંદ્રતા પર બે વિદ્યુતવિભાજ્યોની મોલર વાહકતા નો આધાર $(dependence)$ નીચે આકૃતિમાં દર્શાવેલ છે.$\Lambda \stackrel{\circ}{m}$ એ સિમિત મોલર વાહક્તા છે.View Solution
નીચે આપેલા માંથી ખોટા વિધાન(નો)ની સંખ્યા $..........$ છે.
$(A)$ $\Lambda \stackrel{0}{ m }$ for electrolyte $A$ is obtained by extrapolation
$(B)$ વિદ્યુતવિભાજ્ય $B$ માટે $\Lambda m$ વિરૂદ્ધ $\sqrt{c}$ આલેખ સીધી રેખા મળે છે અને સાથે આંતરછેદ એ $\Lambda \stackrel{0}{ m }$ ને બરાબર (સમાન) છે.
$(C)$ અનંત મંદન પર વિદ્યુતવિભાજ્ય $B$ માટે વિયોજન અંશ નું મૂલ્ય શૂન્ય પ્રસ્થાપિત કરે છે.
$(D)$ વિદ્યુતવિભાજ્ય $A$ અથવા $B$ માટે $\Lambda \stackrel{0}{ m }$ વ્યક્તિગત આયનો માટે $\lambda^{\circ}$ નો ઉપયોગ કરીને ગણતરી કરી શકાય છે ?
- 7View Solutionક્ષારસેતુમાં ...... દ્રાવણ ન ભરી શકાય.
- 8$F{e^{2 + }}/Fe$ અને $S{n^{2 + }}/Sn$ વિદ્યુતધ્રુવ માટે પ્રમાણિત રીડકશન પોટેન્શિયલ ક્રમશ: $ - 0.44$ અને $ - 0.14$ વૉલ્ટ છે.સેલ પ્રક્રિયા $F{e^{2 + }} + Sn\, \to Fe + S{n^{2 + }}$, માટે પ્રમાણિત $EMF$ ...............$\mathrm{V}$ છે.View Solution
- 9નીચેનામાંથી ક્યુ $Al_2(SO_4)_3$ ની તુલ્યવાહકતાને સાચી રીતે રજૂ કરે છે ? $\mathop {{\Lambda _{A{l^{3 + }}}}}\limits^{o\,\,\,\,\,\,\,\,\,\,\,\,\,} $ અને $\mathop {{\Lambda _{SO_4^{2 - }}}}\limits^{o\,\,\,\,\,\,\,\,\,\,\,} $ અનુવર્તી આયનોની અનંત મંદને તુલ્યવાહકતા છે.View Solution
- 10View Solutionએનોડ પર ...... અને કૅથોડ પર ....... પ્રક્રિયા થાય છે.