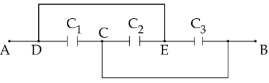
આપેલ સમાંતર પ્લેટ કેપેસીટરના તંત્રને અમુક વિદ્યુતસ્થિમાનના તફાવત વચ્ચે મુકેલ છે. જ્યારે $3\, mm$ જાડાઈ ધરાવતા બ્લોકને કેપેસીટરની પ્લેટ વચ્ચે મૂકવામાં આવે ત્યારે તંત્રમાં સમાન વિદ્યુતસ્થિમાનનો તફાવત જાળવી રાખવા માટે પ્લેટ વચ્ચેના અંતરમાં $2.4\, mm$ જેટલો વધારો કરવામાં આવે છે. તો બ્લોકના દ્રવ્યનો ડાઈઇલેક્ટ્રિક અચળાંક કેટલો હશે?

JEE MAIN 2017, Diffcult
c
Before introducing a slab capacitance of plates
Before introducing a slab capacitance of plates
\(C_{1}=\frac{\varepsilon_{0} A}{3}\)
If a slab of dielectric constant \(K\) is introduced between plates then
\(C=\frac{K \varepsilon_{0} A}{d}\) then \(C'_1 = \frac{{{\varepsilon _0}A}}{{2.4}}\)
\(\mathrm{C}_{1}\) and \({C'}_{1}\) are in series hence,
\(\frac{{{\varepsilon _0}A}}{3} = \frac{{{\text{k}}\frac{{{\varepsilon _0}A}}{3} \cdot \frac{{{\varepsilon _0}A}}{{2.4}}}}{{{\text{k}}\frac{{{\varepsilon _0}A}}{3} + \frac{{{\varepsilon _0}{\text{A}}}}{{2.4}}}}\)
\(3\, k=2.4 \,k+3\)
\(0.6\, \mathrm{k}=3\)
Hence, the dielectric constant of slap is given by,
\(k=\frac{30}{6}=5\)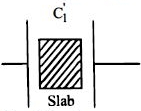
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાંતર પ્લેટ કેપેસીટરની પ્લેટો $100\ V$ સુધી વિદ્યુતભારીત કરેલ છે. હવે $2\ mm$ જાડાઇની પ્લેટને બે પ્લેટો વચ્ચે દાખલ કરવામાં આવે છે તથા સમાન વિદ્યુત સ્થીતીમાન જાળવી રાખવા માટે કેપેસીટરની બે પ્લેટો વચ્ચેનું અંતર $1.6\, mm $ વધારવામાં આવે તો પ્લેટનો ડાઇ ઇલેકટ્રીક અચળાંક....View Solution
- 2$Y$ અક્ષ પર આવેલા બે બિંદુઓ $A$ અને $B$ ઊગમબિંદુથી $12.3\ cm$ . અને $12.5\ cm$ અંતરે આવેલા છે. આ બિંદુઓ આગળ સ્થિતમાન અનુક્રમે $56\, V$ અને $54.8 \,V$ છે. $Y$ અક્ષ પરના બિંદુ $A$ આગળ $4\ \mu C$ નો વિદ્યુતભાર મૂકતાં તેના પર બળનો કયો ઘટક હશે ?View Solution
- 3$A$ ક્ષેત્રફળ અને $Q$ વિદ્યુતભાર ધરાવતા સમાંતર પ્લેટ કેપેસિટરની ઊર્જા ઘનતા કેટલી થાય?View Solution
- 4એક ક્ષેત્રમાં એકસમાન વિદ્યુતક્ષેત્ર પ્રવર્તે છે. આ ક્ષેત્રમાં બિંદુ $P$ આગળ કેન્દ્ર હોય તેવા ગોળા પરના અલગ અલગ બિંદુ આગળનું વિદ્યુતસ્થિતિમાન $589.0\,V$ થી $589.8\, V$ જેટલું બદલાય છે. વિદ્યુતક્ષેત્ર સાથે $60^o$ નો ખુણો બનાવતા સ્થાન સદીશ પર રહેલ ગોળા પરના બિંદુ આગળ વિદ્યુતસ્થિતિમાન ($V$ માં) કેટલું હશે?View Solution
- 5View Solutionસ્થિતિમાનના તફાવતનું પારિમાણિક સૂત્ર ........ છે.
- 6બે સમાંતર પ્લેટો વચ્ચેનું અંતર તથા દરેક પ્લેટનું ક્ષેત્રફળ $A$ છે જ્યારે $K$ ડાઇઇલેક્ટ્રીક અચળાંક અને $t$ જાડાઇના સ્લેબ ને પ્લેટોની વચ્ચે મુકવામાં આવે તો નવુ કેપેસીટન્સ....View Solution
- 7એક ઓટોમોબાઈલ સ્પ્રિંગ $5000\, N$ લોડ માટે $0.2\ m$ સુધી વધે છે. તો આ સ્પ્રિંગ $0.2\ m$ જેટલી સંકોચાયેલી હોય ત્યારે સંગ્રહિત સ્થિતિ ઊર્જા અને $10000\, V$ ના સ્થિતિમાન તફાવતે $10\ \mu F$ કેપેસિટરમાં સંગ્રહિત સ્થિતિ ઉર્જાનો ગુણોત્તર કેટલો હશે ?View Solution
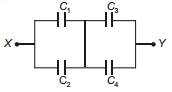
- 8આકૃતિમાં $C_1=10 \mu F , C_2=C_3=20 \mu F$, અને $C_4=$ $40 \mu F$ દર્શાવેલ છે. જો $C_1$ પર $20 \mu C$ જેટલો ચાર્જ રહેલો હોય તો બિંદુ $X$ અને $Y$ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત શોધો.View Solution
- 9બે પ્લેટો એકબીજાથી $20\, cm$ દૂર છે. તેમની વચ્ચે વિદ્યુુત સ્થિતિમાનનો તફાવત $10\, volt$ છે, તો બે પ્લેટો વચ્ચે વિદ્યુતક્ષેત્ર ......$Vm^{-1}$View Solution
- 10View Solutionપોલા ધાતુના પાત્રમાંના અંદરના વિદ્યુતભારિત બિંદુ આગળ વિદ્યુતક્ષેત્રની તીવ્રતા ....... છે.
