અચળ $e.m.f$ ધરાવતા વિધુત કોષને પહેલા અવરોધ $R_1$ અને ત્યારબાદ અવરોધ $R_2$ સાથે જોડવામાં આવે છે. જો બંને કિસ્સામાં વપરાતો પાવર સમાન હોય તો વિધુતકોષનો આંતરીક અવરોધ કેટલો હશે ?
Diffcult
Download our app for free and get started
a
વય્ય થતો પાવર \(\, = \,\,{i^2}R\,\, = \,\,{\left( {\frac{E}{{R\, + \,r}}} \right)^2}\,R\)
વય્ય થતો પાવર \(\, = \,\,{i^2}R\,\, = \,\,{\left( {\frac{E}{{R\, + \,r}}} \right)^2}\,R\)
\(\therefore \,\,\,{\left( {\frac{E}{{{R_1}\, + \,r}}} \right)^2}\,{R_1}\,\, = \,\,{\left( {\frac{E}{{{R_2}\, + \,r}}} \right)^2}\,{R_2}\)
\( \Rightarrow \,{R_1}\,(R_2^2\, + \,{r^2}\, + \,2{R_2}^r)\,\, = \,\,{R_2}\,(R_1^2\, + \,{r^2}\, + \,2{R_1}r)\)
\( \Rightarrow \,R_2^2{R_1}\, + \,{R_1}{r^2}\, + \,2{R_1}\,{R_2}r\,\, = \,\,R_1^2\,{R_2}\, + \,{R_2}{r^2}\, + \,2{R_1}\,{R_2}r\)
\( \Rightarrow \,{({R_1}\, - \,{R_2})^2}\, = \,\,({R_1}\, - \,{R_2})\,{R_1}\,{R_2}\,\,\, \Rightarrow \,\,r\,\, = \,\,\sqrt {{R_1}\,{R_2}} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
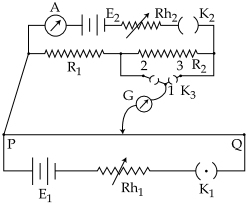
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે બે અવરોધની સરખામણી કરવા માટે પોટેન્શિયોમીટર $PQ$ વાપરવામાં આવે છે. જ્યારે કળ $K_3$ ખુલ્લી હોય ત્યારે $A$ એમીટર $1.0\, A$ નો પ્રવાહ દર્શાવે છે. જ્યારે કળ $K_3$ ને $2$ અને $1$ વચ્ચે જોડેલી હોય ત્યારે તટસ્થ બિંદુ $P$ થી $l_1\, cm$ અંતરે મળે છે, જ્યારે કળ $K_3$ ને $3$ અને $1$ વચ્ચે જોડેલી હોય ત્યારે તટસ્થ બિંદુ $P$ થી $l_2\, cm$ અંતરે મળે છે. તો બંન્ને અવરોધનો ગુણોત્તર $\frac{{{R_1}}}{{{R_2}}}$ કેટલો મળે?View Solution
- 2$400\, \Omega$ અને $800\, \Omega$ ના અવરોધકને $6 V$ ની બેટરી સાથે શ્રેણીમાં જોડેલ છે. $10\, k \Omega$ અવરોધ, ધરાવતુ વૉલ્ટમીટરને $400\, \Omega$ અવરોધને સમાંતર લગાવતા તેનુ અવલોકન .......... $V$View Solution
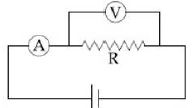
- 3આકૃતિમાં દર્શાવેલ અવરોધ $R$ નું વાસ્તવિક મુલ્ય $30\Omega$ છે. આનું માપન એક પ્રયોગ દ્વારા $R =\frac{V}{I}$ ના પ્રમાણિત સંબંધથી માપવામાં આવે છે, જ્યાં $V$ અને $I$ એ અનુક્રમે વોલ્ટમીટર અને એમીટરના વાંચનો છે. જો માપવામાં આવેલ $R$ નું મૂલ્ય $5\%$ ઓછુ હોય, તો આ વોલ્ટમીટરનો આંતરિક અવરોધ ............ $\Omega$ હશે.View Solution
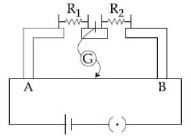
- 4આકૃતિમાં બતાવેલ મીટરબ્રીજનાં પ્રયોગની ગોઠવણમાં બિંદુ $A$ થી $40\, cm$ ના અંતરે તટસ્થ બિંદુ મળે છે. હવે જો $10\,\Omega$ ના અવરોધને $R_1$ સાથે શ્રેણીમાં જોડવામાં આવે, તો તટસ્થ બિંદુ $10\, cm$ જેટલું ખસે છે. હવે જો તટસ્થ બિંદુને પાછું તેની પ્રારંભિક સ્થિતિમાં લાવવુ હોય તો અવરોધ $(R_1 +10)\,\Omega$ ને સમાંતર કેટલા ................ $\Omega$ અવરોધ જોડવો પડે ?View Solution
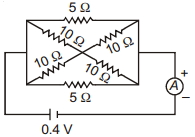
- 5આાપેલ સર્કીટ ડાયાગ્રામમાં એમીટર $A$ વડે દશર્વવામાં આવતો વિદ્યુતપ્રવાહ .......... $A$.View Solution
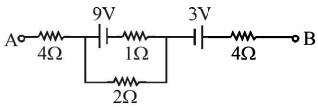
- 6નીચે આપેલા આકૃતિમાં બિંદુ $A$ અને $B$ વચ્ચેનો તફાવત $16\,v$ છે. $2\,\Omega$ માંથી પસાર થતો પ્રવાહ $...........\,A$View Solution
- 7$5\,A$ ના ફ્યુઝનો ઉપયોગ કરીને $220\,V$ પર $60\,W$ બલ્બ સલામત રીતે ચલાવી શકાય?View Solution
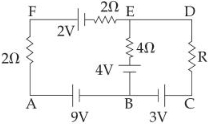
- 8આપેલ પરિપથમાં રહેલ $4\, \Omega $ અવરોધમાંથી પ્રવાહ પસાર ન થતો હોય તો તે સમયે બિંદુ $A$ અને બિંદુ $D$ વચ્ચે વિદ્યુતસ્થિતિમાનનો તફાવત કેટલા ................. $V$ હશે?View Solution
- 9વાહકમાંના પ્રવાહને $\mathrm{I}=3 \mathrm{t}^2+4 \mathrm{t}^3$ જ્યાં $\mathrm{IA}$ માં અને $\mathrm{t}$ સેકન્ડમાં છે, વડે રજૂ કરવામાં આવે છે. તો $\mathrm{t}=1 \mathrm{~s}$ થી $\mathrm{t}=2 \mathrm{~s}$ દરમિયાન વાહકના વિભાગ (છેદ) માંથી વહેતો વીજભારનો જથ્યો_______$C$છે.View Solution
- 10$6$ વોલ્ટની બેટરી $100\,\Omega$ અવરોધ અને ત્રણ મીટરના લાંબા તારના છેડા સાથે જોડાયેલ છે. તારમાં $50 \,cm$ અંતરે રહેલા બિંદુ વચ્ચેનો સ્થિતિમાનનો તફાવત .............. $V$ હશેView Solution