અચળ વેગથી જતી ખુલ્લી કારમાં માણસ દડાને ઉપર તરફ ફેંકે છે,તો દડો
Easy
d
(d)Horizontal velocity of ball and person are same so both will cover equal horizontal distance in a given interval of time and after following the parabolic path the ball falls exactly in the hand which threw it up.
(d)Horizontal velocity of ball and person are same so both will cover equal horizontal distance in a given interval of time and after following the parabolic path the ball falls exactly in the hand which threw it up.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પદાર્થ પર $10\;N$ બળ લાગતાં તેમાં $1 \;m / s ^{2} $ નો પ્રવેગ ઉત્પન્ન થાય તો આ પદાર્થનું દળ ($kg$ માં) કેટલું હશે?View Solution
- 2એક તારના ટુકડાને $Y = Kx^2$ અનુસાર પરવલય આકારમાં વાળવામાં આવેલ છે. તેની અંદર $m$ દળનું એક જંતુ છે, જે તાર પર ઘર્ષણરહિત સરકી શકે છે. જ્યારે તાર સ્થિર હોય ત્યારે તે પરવલયના સૌથી નીચેના બિંદુ પાસે છે. હવે તારને $ X-$ અક્ષને સમાંતર વલય જેટલા અચળ પ્રવેહથી ગતિ કરાવવામાં આવે છે, તો હવે જંતુ તારની સાપેક્ષે સ્થિર રહી શકે તેવું નવા સંતુલિત સ્થાનનું $ Y-$ અક્ષથી અંતર કેટલું હશે ?View Solution
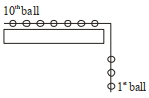
- 3દરેક $2 \,kg$ ના $10$ બોલના બનેલાં તંત્રને દળરહિત અને ખેંચી ના શકાય તેવી દોરી વડે જોડવામાં આવેલા છે. આ તંત્રને લીસા ટેબલ ઉપર આફૃતિમાં દર્શાવ્યા અનુસાર સરકવા દેવામાં આવે છે. જ્યારે છઠ્ઠો બોલ ટેબલને છોડે તે જ ક્ષણે $7^{\text {th }}$ મા અને $8^{\text {th }}$ મા બોલ વચ્યે દોરીમાં તણાવ ........... $N$ હશે.View Solution
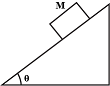
- 4$M$ દળનો એક બ્લોકને ઘર્ષણરહિત લીસા ઢાળ પર પડેલો છે. દળને મુકત કરીને ઢાળને કેટલો પ્રવેગ $a$ આપવો પડે કે જેથી $M$ દળ સ્થિર રહે?View Solution
- 5${m_1},\,{m_2}$ અને ${m_3}$ દળના બ્લોકને વજનરહિત દોરી વડે બાંઘીને ઘર્ષણરહિત સપાટી પર મૂકેલાં છે. $m_3$ દળ પર $T$ બળ લગાડવામાં આવે,તો ${m_2}$ અને ${m_3}$ વચ્ચેની દોરીમાં તણાવ કેટલો થશે?View Solution
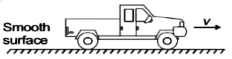
- 6એક બંદૂકધારીનું, બંદૂક સાથેનું દળ $100\,kg$ છે, જે સરળ સપાટી પર ઉભેલો છે અને $10 \,shot$ સમક્ષિતિજ રીતે છોડે છે. દરેક ગોળીનું દળ $10\,g$ છે. અને બંદૂકનો વેગ $800\,m / s$ છે. $10\,shot$ છોડયા.પછી બંદૂકધારી $..........\,ms^{-1}$ વેગ મેળવશે.View Solution
- 7એક $9 \,kg$ દળનો બોમ્બ $3 \,kg$ અને $6 \,kg$ નાં બે ટુકડાઓમાં ફાટે છે. જો $3 \;kg$ વાળા દળનો વેગ $16 \,m / s$ છે.તો $6 \,kg$ વાળા દળની ગતિઉર્જા જૂલમાં કેટલી હશે?View Solution
- 8એક રેતીથી ભરેલી ગાડી $v$ વેગ સાથે ગતિ કરી રહી છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે રેતી છિદ્રમાંથી પડી રહી છે તો જમીન પર પડ્યા પછી. રેતી....View Solution
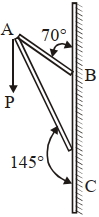
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે બે દળરહિત સળિયા $AB$ અને $AC$ દ્વારા એક ફ્રેમ બનાવેલ છે. $A$ બિંદુ પર $\overrightarrow{ P }$ બળ લાગે છે જેનું મૂલ્ય $100\; N$ છે. તો બળ $\overrightarrow{ P }$ નો $AC$ ની દિશામાંનો ઘટક $x\;N$ હોય તો $x$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે?View Solution
[$\sin \left(35^{\circ}\right)=0.573, \cos \left(35^{\circ}\right)=0.819$ $\left.\sin \left(110^{\circ}\right)=0.939, \cos \left(110^{\circ}\right)=-0.342\right]$
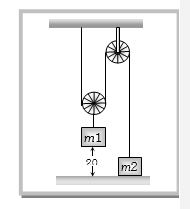
- 10જો $ m_1 = 4m_2$ હોય,તો $m_1 $ નો પ્રવેગ $a$ છે. $a =$ ____View Solution