એક બંદૂકધારીનું, બંદૂક સાથેનું દળ $100\,kg$ છે, જે સરળ સપાટી પર ઉભેલો છે અને $10 \,shot$ સમક્ષિતિજ રીતે છોડે છે. દરેક ગોળીનું દળ $10\,g$ છે. અને બંદૂકનો વેગ $800\,m / s$ છે. $10\,shot$ છોડયા.પછી બંદૂકધારી $..........\,ms^{-1}$ વેગ મેળવશે.
Easy
Download our app for free and get started
b
(b)
(b)
According to law of conservation of momentum,
\(100\,v =-\frac{10}{1000} \times 10 \times 800\)
i.e., \(v=0.8\,ms ^{-1}\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
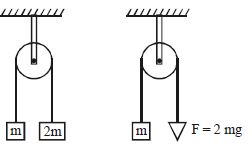
- 1બે સમાન ગરગડી ને આકૃતિ માં બતાવ્યા મુજબ ગોઠવેલી છે. દોરડાનું દળ અવગણ્ય છે.આકૃતિ $(a)$ માં $m$ દળને દોરડાના બીજા છેડા સાથે $2\,m$ દળને જોડીને ઊંચકવામાં આવે છે. આકૃતિ $(b)$ માં $m$ દળને બીજા છેડા પર નીચે તરફ $F = 2mg$ જેટલું અચળ ખેંચાણ લગાડી ને ઊંચકવામાં આવે છે. તો બંને કિસ્સામાં $m$ નો પ્રવેગ અનુક્રમે શું થાય?View Solution
- 2View Solutionજ્યારે ઘોડો ડબ્બાને ખેંચતો હોય ત્યારે ઘોડો આગળ તરફ ગતિ કરે તે કયા બળ ને લીધે કરે?
- 3$60 \,kg$ નો એક વ્યક્તિ રસ્તા ઉપર દોડે છે અને એકદમ જ $120 \,kg$ દળ ધરાવતી સ્થિર ટ્રોલી કારમાં કૂદકો મારે છે. પછી, ટ્રોલી કાર $2 \,ms ^{-1}$ ના વેગથી ગતિ કરવાનું શરૂ કરે છે. જ્યારે માણસ કારની અંદર કૂદકો મારે છે ત્યારે દોડતા માણસનો વેગ ............ $ms ^{-1}$ હશે.View Solution
- 4${m_1},\,{m_2}$ અને ${m_3}$ દળના બ્લોકને વજનરહિત દોરી વડે બાંઘીને ઘર્ષણરહિત સપાટી પર મૂકેલાં છે. $m_3$ દળ પર $T$ બળ લગાડવામાં આવે,તો ${m_2}$ અને ${m_3}$ વચ્ચેની દોરીમાં તણાવ કેટલો થશે?View Solution
- 5View Solutionએક દોડવીર વિજેતા રેખાને પાર કર્યા બાદ શા માટે તરત ઉભો નથી રહી જતો.
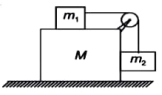
- 6આપેલી પરિસ્થિતિમાં દર્શાવેલી તમામ સપાટીઓ લીસી છે. તો તંત્રને શું પ્રવેગ આપવો જોઈએ કે, જેથી $m_2$ બ્લોક નીચે તરફ ગતિ ન કરે?View Solution
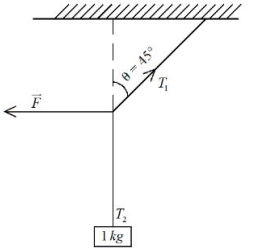
- 7$1 \mathrm{~kg}$ દળને છત પરથી $4m$ લંબાઈના દોરડાથી લટકાવવામાં આવેલ છે. આકૃત્તિમાં દર્શાવ્યા અનુસાર દોરડાના મધ્યબિંદુ આગળ સમક્ષિતિજ બળ $'F$ લગાડતા દોરડું શિરોલંબ અક્ષને સાપેક્ષ $45^{\circ}$ નો કોણ બનાવે છે. $F$નું મૂલ્ય ......... હશે. (એવું ધારોકે દળ સમતોલન સ્થિતિમાં છે અને $g=10 \mathrm{~m} / \mathrm{s}^2$ છે.)View Solution
- 8$200 \,m / s$ ની ગતિથી ચાલતી $10 \,g$ દળની એક ગોળી લાકડાના પાટિયામાં $5 \,cm$ સુધી ઘૂસીને અટકી જાય છે. ગોળી પર લાગેલો સરેરાશ બળ ................ $N$ હશે.View Solution
- 9$M$ દળ અને $L$ લંબાઈની એકરૂપ દોરીને તેનાં ઉપરનાં સંતિમ છેડાને દઢ આધાર સાથે શિરોલંબ રીતે જોડેલ છે. તો પછી દઢ આધારથી $l$ અંતર પર દોરીમાં ઉદભવતો તણાવ શોધો.View Solution
- 10લિફ્ટમાં સ્પ્રિંગ બેલેન્સ પર $2\, kg$ નો દળ લટકાવેલ છે. હવે લિફ્ટ $2 \,m/sec^2$ ના પ્રવેગથી ઉપર તરફ ગતિ કરે, તો સ્પ્રિંગ બેલેન્સનું અવલોકન ....... $kg$ હશે.View Solution