એક તારના ટુકડાને $Y = Kx^2$ અનુસાર પરવલય આકારમાં વાળવામાં આવેલ છે. તેની અંદર $m$ દળનું એક જંતુ છે, જે તાર પર ઘર્ષણરહિત સરકી શકે છે. જ્યારે તાર સ્થિર હોય ત્યારે તે પરવલયના સૌથી નીચેના બિંદુ પાસે છે. હવે તારને $ X-$ અક્ષને સમાંતર વલય જેટલા અચળ પ્રવેહથી ગતિ કરાવવામાં આવે છે, તો હવે જંતુ તારની સાપેક્ષે સ્થિર રહી શકે તેવું નવા સંતુલિત સ્થાનનું $ Y-$ અક્ષથી અંતર કેટલું હશે ?
Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ગતિ કરતાં માલવાહક પટ્ટા પર $M\ kg/s $ ના દરથી રેતી પાડવામાં આવે છે. જો પટ્ટાનો અચળ વેગ $v\ m/s $ જાળવી રાખવો હોય,તો પટ્ટા પર કેટલું બળ લગાડવું જરૂરી છે?View Solution
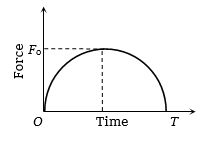
- 2સ્થિર સ્થિતિમાં રહેલા $m$ દળના કણ પર લાગતા બળનો આલેખ આપેલ છે.બળ બંધ થયા પછી તેનો વેગ $u$ હોય તો $u$ કેટલો થાય?View Solution
- 3હાઇડ્રોજન અણુનું દળ $3.32 \times 10^{-27 } $ $kg$ છે.જો $10^{23}$ હાઇડ્રોજન અણુઓ બીજી પ્રતિ સેકન્ડ, $2$ $cm^2$ ક્ષેત્રફળ ધરાવતી જડિત દિવાલ ઉપર તેના લંબને $45^o $ ના કોણે આપાત થાય છે.અને સ્થિતિસ્થાપક રીતે $10^3$ $ m/s$ ની ઝડપ સાથે પાછા ફરે છે.તો દિવાલ ઉપરનું દબાણ લગભગ ________ થશે.View Solution
- 4એક બેટ્સમેન $0.4 \,kg$ દળ ધરાવતા બોલને પાછો બોલરની જ દિશામાં તેની પ્રારંભિક ઝ5પ $15 \,ms ^{-1}$ ને બદલ્યા વગર ફટકારે છે. બોલને આપવામાં આવતો આવેગ (બોલને રેખીય ગતિ છે તેમ ધારતાં) ......... $Ns$ હશે.View Solution
- 5લીસી હલકી ગરગડી પરથી પસાર થતી એક હલકી દોરી $m_1$ અને $m_2$ દળોનાં બે ચોસલાઓને બાંધે છે. જો તંત્રનો પ્રવેગ $\frac{g}{8}$ હોય તો, દળોનો $\frac{\mathrm{m}_2}{\mathrm{~m}_1}$ ગુણોત્તર :View Solution
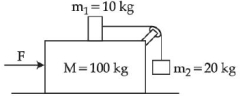
- 6આકૃતિમાં દર્શાવ્યા અનુસાર ત્રણ દળો $M =100\,kg , m _1=10\,kg$ અને $m _2=20\,kg$ ને ગોઠવવામાં આવ્યા છે. બધીજ સપાટીઓ ઘર્ષણરહિત અને દોરીઓ ખેંચાણ અનુભવતી નથી અને હલકી છે. પુલી પણ હલકી અને ઘર્ષણરહિત છે. તંત્ર પર બળ $F$ એવી રીતે સગાવવામાં આવે છે કે જેથી દળ $m _2,\; 2 \;ms ^{-2}$ ના પ્રવેગથી ઉપરની તરફ ગતિ કરે છે. બળ $F$ નું મૂલ્ય $............N$ થશે( $g =10 ms ^{-2}$ લો.)View Solution
- 7સ્થિર લિફ્ટમાં માણસનો વજન અને નીચે તરફ $‘a’$ પ્રવેગથી ગતિ કરતી લિફ્ટમાં માણસના વજનનો ગુણોત્તર $3 : 2$ હોય,તો $‘a’$ = _____View Solution
- 8View Solutionનીચે આપેલી બળની જોડ સમતુલનમાં છે.
- 9$1 \;kg$ દળવાળા પદાર્થને ઊઘ્વૅ દિશામાં $100 \;m / s$ ના વેગથી ફેંકવામાં આવે છે. $5 \;seconds$ બાદ તે બે ટુકડાઓમાં વિભાજિત થાય છે. $400\; g$ દળવાળો એક ટુકડો અધોદિશામાં $25 \;m / s$ ના વેગથી ફેંકાય છે. બીજા ટુકડાના વેગની ગણતરી કરો?View Solution
- 10એક લિફ્ટ $a$ જેટલા પ્રવેગથી નીચે આવી રહી છે.લિફ્ટમાં ઊભેલી વ્યકિત એક બોલ પડતો મૂકે છે,તો લિફ્ટમાં ઊભેલી વ્યકિત અને બહાર જમીન પર ઊભલી વ્યકિત તે આ બોલના પ્રવેગ અનુક્રમે _______ અને ________ માપશેView Solution