An aeroplane leaves an airport and flies due north at a speed of $1000\ km$ per hour. At the same time, aeroplane leaves the same airport and flies due west at a speed of $1200\ km$ per hour. How far apart will be the two planes after $1\frac{1}{2}\text{hour}?$
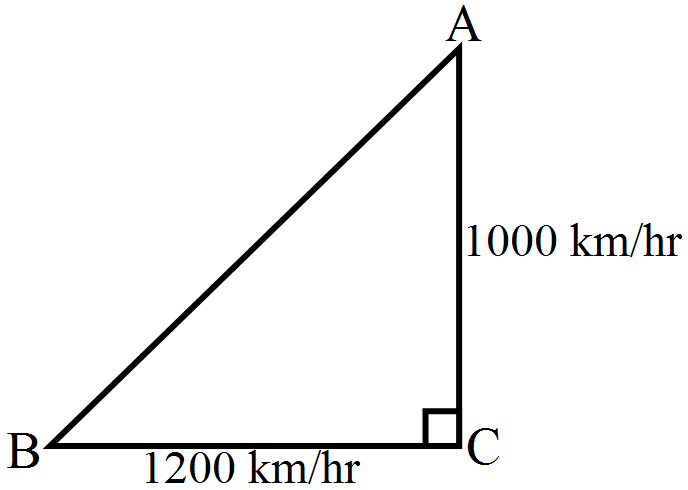
Let $C$ be the airport and let $A$ and $B$ be the two aerplanes flying north and west respectively Distance covered by $A$ in $1\frac{1}{2}=\frac{3}{2}\text{hours}$
$= AC$
$=1000\times\frac{3}{2}=1500\text{km}$
Distance covered by B in $1\frac{1}{2}=\frac{3}{2}\text{hours}$ hours
$= BC$
$=1200\times\frac{3}{2}=1800\text{km}$
In $\triangle\text{ABC},$
By Pythagoras theorem,
$AB^2 = AC^2 + BC^2$
$\Rightarrow AB^2= 1500^2 + 1800^2$
$\Rightarrow AB^2 = 2250000 + 3420000$
$\Rightarrow AB^2 = 5490000$
$\Rightarrow\text{AB}=300\sqrt{61}\text{km}$
Hence, after $1\frac{1}{2}$ hours, the planes $ A$ and $B$ are $300\sqrt{61}\text{km}$ apart.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
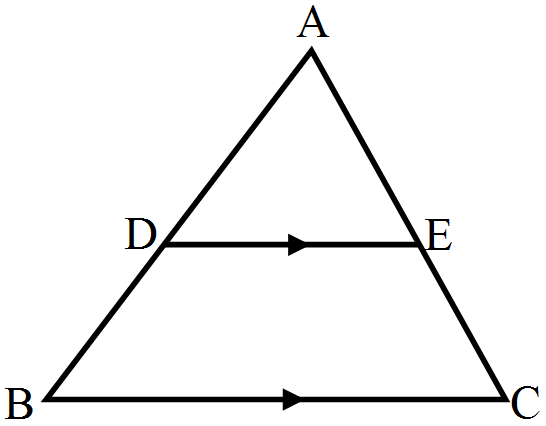
- 1D and E are points on the sides AB and AC respectively of a $\triangle\text{ABC}$ such that DE || BC:View Solution
AD = (7x - 4)cm, AE = (5x - 2)cm, DB = (3x + 4)cm and EC = 3x cm.
- 2View SolutionThe corresponding altitudes of two similar triangles are 6cm and 9cm respectively, Find the ratio of their areas.
- 3Find the length of altitude AD of an isosceles $\triangle\text{ABC}$ in which AB = AC = 2a units and BC = a units.View Solution
- 4View SolutionA vertical pole of lenght 7.5m casts a shadow 5m long on the ground and at the same time a tower casts a shadow 24m long. Find the height of the tower.
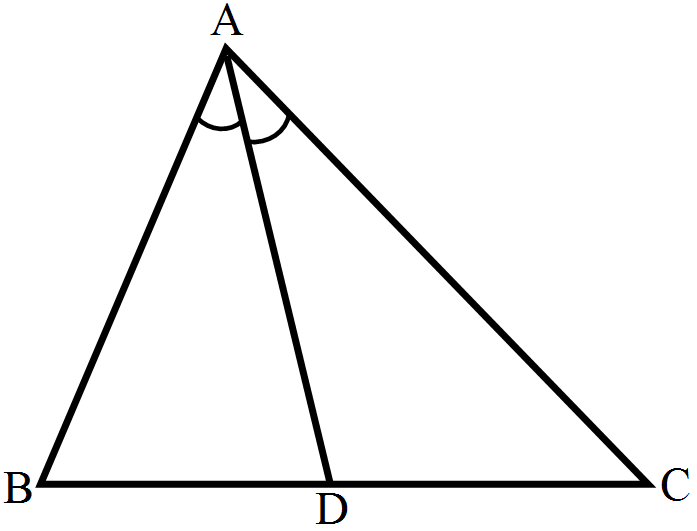
- 5In a $\triangle\text{ABC},\text{AD}$ is the bisector of $\angle\text{A}.$View Solution
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.
- 6View SolutionFind the lenght of each side of a rhombus whose diagonals are 24cm and 10cm. long.
- 7If the lengths of the sides BC, CA and AB of a $\triangle\text{ABC}$ are a, b and c respectively and AD is the bisectore of $\angle\text{A}$ then find the lengths of BD and DC.View Solution
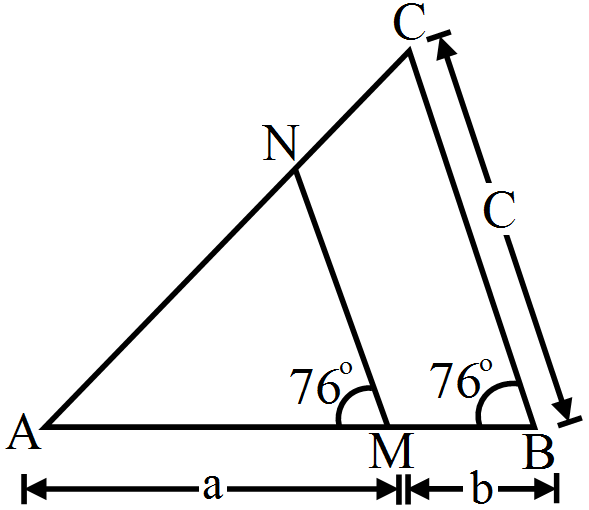
- 8In the given figure, $\angle\text{AMN}=\angle\text{MBC}=76^\circ.$ If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN in terms of p, q and r.View Solution
- 9$\triangle\text{ABC}$ is an isosceles triangle with $AB = AC = 13\ cm$. The length of altitude from $A$ on $BC$ is $5\ cm$. Find $BC$.View Solution
- 10$\triangle\text{ABC}\sim\triangle\text{PQR}$ and $\text{ar}(\triangle\text{ABC})=4\text{ar}(\triangle\text{PQR}).$ If BC 12cm, find QR.View Solution
