In the given figure, $\angle\text{AMN}=\angle\text{MBC}=76^\circ.$ If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN in terms of p, q and r.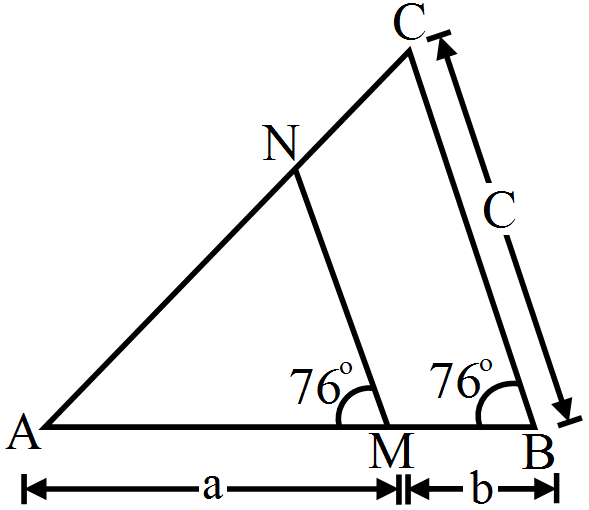

In $\triangle\text{ABC}$ and $\triangle\text{AMN},$
$\angle\text{M}=\angle\text{B}=76^\circ$ .....(corresponding angles)
and $\angle\text{BAC}=\angle\text{MAN}$ .....(common angle)
$\Rightarrow\triangle\text{ABC}\sim\triangle\text{AMN}$ .....(AA criterion)
$\frac{\text{AB}}{\text{AM}}=\frac{\text{BC}}{\text{MN}}$
$\frac{\text{AM}+\text{MB}}{\text{AM}}=\frac{\text{BC}}{\text{MN}}$
$\frac{\text{a}+\text{b}}{\text{a}}=\frac{\text{c}}{\text{MN}}$
$\Rightarrow\text{MN}=\frac{\text{ac}}{\text{a}+\text{b}}$
$\angle\text{M}=\angle\text{B}=76^\circ$ .....(corresponding angles)
and $\angle\text{BAC}=\angle\text{MAN}$ .....(common angle)
$\Rightarrow\triangle\text{ABC}\sim\triangle\text{AMN}$ .....(AA criterion)
$\frac{\text{AB}}{\text{AM}}=\frac{\text{BC}}{\text{MN}}$
$\frac{\text{AM}+\text{MB}}{\text{AM}}=\frac{\text{BC}}{\text{MN}}$
$\frac{\text{a}+\text{b}}{\text{a}}=\frac{\text{c}}{\text{MN}}$
$\Rightarrow\text{MN}=\frac{\text{ac}}{\text{a}+\text{b}}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View SolutionIn the given pairs of triangles, find which pair of triangles are similar. State the similarity criterior and write the similarity relation in symbolic from.
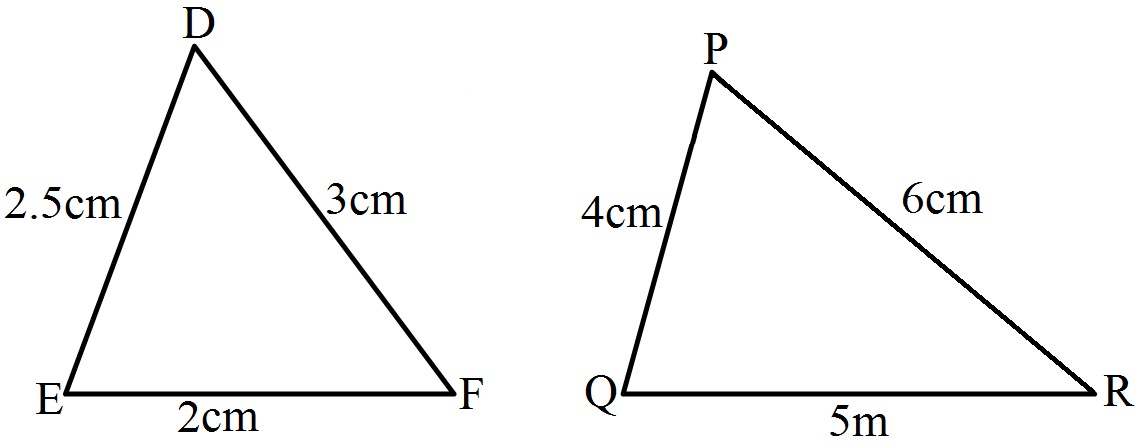
- 2View SolutionFind the height of an equilateral triangle of side 12cm.
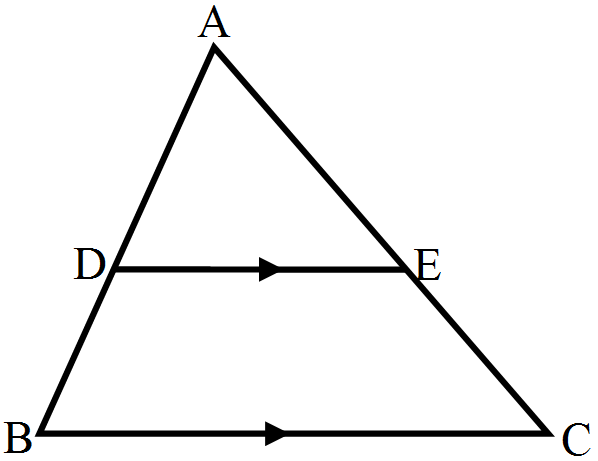
- 3D and E are points on the sides AB and AC respectively of a $\triangle\text{ABC}$ such that DE || BC: If $\frac{\text{AD}}{\text{AB}}=\frac{8}{15}$ and EC = 3.5cm, find AE.View Solution
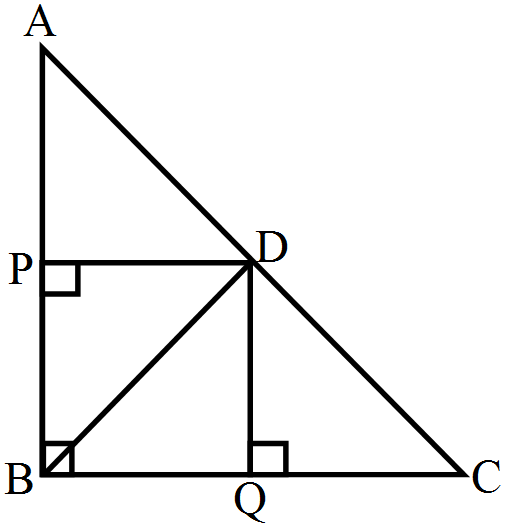
- 4In a right triangle $ABC,$ right-angled at $B, D$ is a point on hypotenuse such that $\text{BD}\perp\text{AC}.$ If $\text{DP}\perp\text{AB}$ and $\text{DQ}\perp\text{BC}$ then prove that.View Solution
- $\text{DQ}^2=\text{DP}.\text{DQ}$
- $\text{DP}^2=\text{DQ}.\text{AP}$
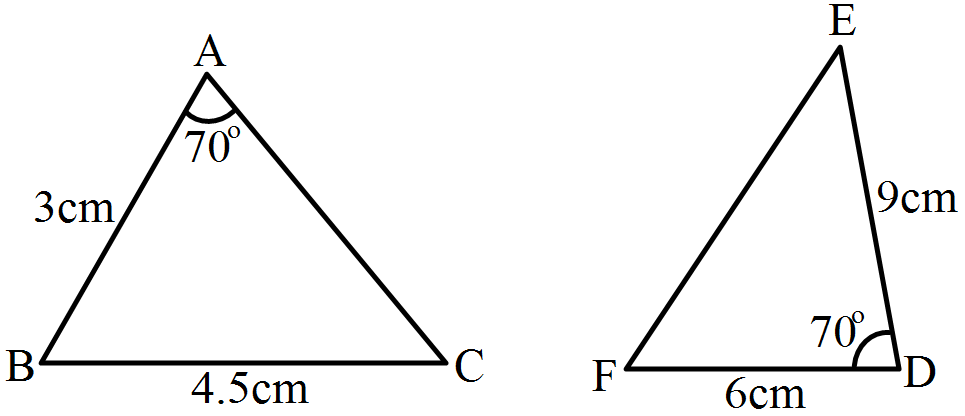
- 5View SolutionIn the given pairs of triangles, find which pair of triangles are similar. State the similarity criterior and write the similarity relation in symbolic from.
- 6View SolutionFind the lenght of each side of a rhombus whose diagonals are 24cm and 10cm. long.
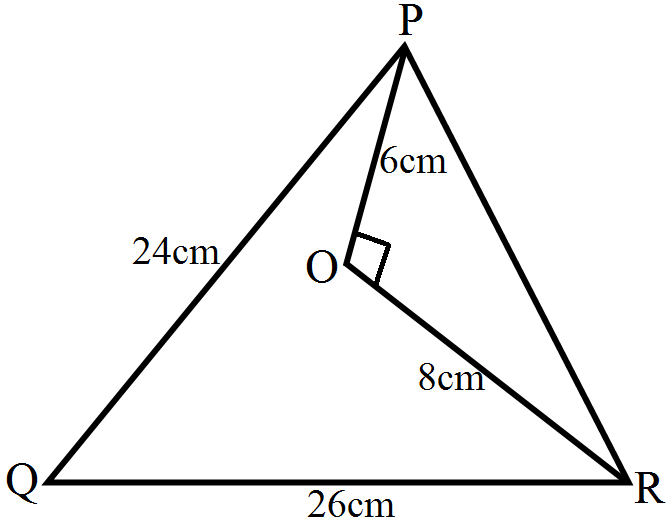
- 7In the given figure, O is a point inside a $\triangle\text{PQR}$ such that $\angle\text{PQR}=90^\circ,\text{OP}=6\text{cm}$ and $\text{OR}=8\text{cm}.$ If $\text{PQ}=24\text{cm}$ and $\text{QR}=26\text{cm},$ prove that $\triangle\text{PQR}$ is right-angled.View Solution
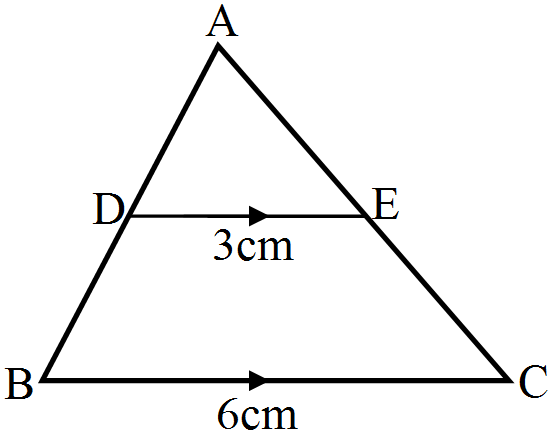
- 8In the given figure, $DE || BC$. If $DE = 3\ cm$, $BC = 6\ cm$ and $\text{ar}(\triangle\text{ADE})=15\text{cm}^2,$ find the area of $\triangle\text{ABC}.$View Solution
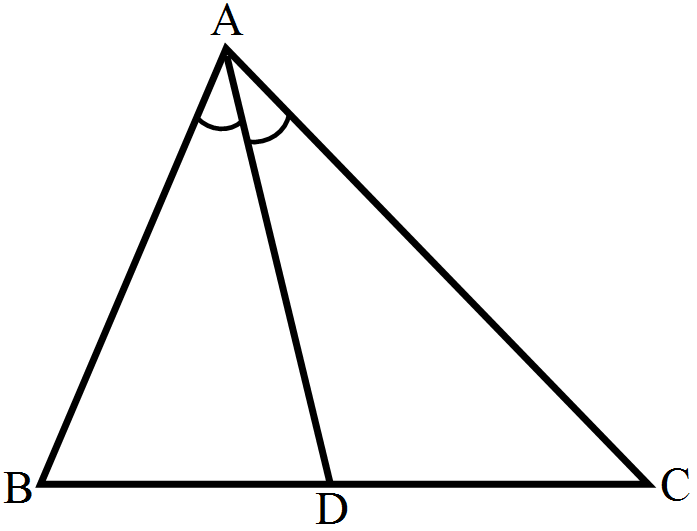
- 9In a $\triangle\text{ABC},\text{AD}$ is the bisector of $\angle\text{A}.$ If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.View Solution
- 10$\triangle\text{ABC}\sim\triangle\text{PQR}$ and $\text{ar}(\triangle\text{ABC})=4\text{ar}(\triangle\text{PQR}).$ If BC 12cm, find QR.View Solution
