અંતર્ગોળ અરીસા દ્વારા રચાતું પ્રતિબિંબ . . . . .
Easy
c
Using mirror equation,
Using mirror equation,
\(\frac{1}{ v }+\frac{1}{ u }=\frac{1}{ f }\)
\(\frac{1}{ v }=\frac{1}{ f }-\frac{1}{ u }\)
For concave mirror, focal length is negative. Hence, \(f<0\)
For a virtual object, object distance is positive. Hence \(u _v>0\)
From above, it can be observed that image distance \(v\) is negative when object is virtual. Since image distance is negative, it is formed by real intersection of rays and image is real.
For a real object, object distance is negative. Hence \(u _{ r }<0\)
In this case, image distance \(v\) may be positive or negative depending on the location of object.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક છોકરો $30 \,cm$ દૂર રહેલા અરીસાની સામે ઉભો છે. તેના ચત્તું પ્રતિબિંબનું ઉંચાઈ તેની વાસ્તવિક ઉંચાઈથી $\frac{1}{5}^{th}$ ભાગની છે. તેણે ઉપયોગમાં લીધેલો અરીસો ..... .છે.View Solution
- 2એક વિદ્યાર્થી બહિર્ગોળ લેન્સથી $'u'$ અંતરે વસ્તુ પિનનુ $'v'$ અંતરે પ્રતિબિંબ મેળવીને કેન્દ્રલંબાઈ માપે છે અને પિનના પ્રતિબિંબનું અંતર$ 'v' $ પામે છે.$ 'u'$ અને $'v'$ વચ્ચેનો આલેખ કેવો મળશે?View Solution
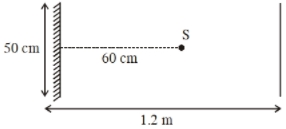
- 3પ્રકાશનો બિંદુવત ઉદગમ $S, 50\, cm$ પહોંળાઈ ધરાવતા દિવાલ પર શિરોલંબ લટકાવેલ સાદા અરીસાના કેન્દ્રની સામે $60\, cm$ ના અંતરે ગોઠવાયેલો છે. આકૃતિમાં દર્શાવ્યા મુજબ એક માણસ આ અરિસાથી $1.2\, m$ દૂરના અંતરે, અરીસાને સમાંતર લીટી પર ચાલે છે. અરીસામાં દષ્યમાન પ્રકાશનું પ્રતીબિંબ, ચરમ બિંદુઓ (extreme points) થી .......$cm$ અંતરે આવેલ છે.View Solution
- 4જો બહિર્ગોળ સપાટીની વક્રતા ત્રિજ્યા $10\,\, cm $ હોય અને લેન્સની કેન્દ્રલંબાઈ $30\,\, cm$ હોય, તો સમતલીય બહિર્ગોળ લેન્સના પદાર્થનો વક્રીભવનાંક કેટલો છે?View Solution
- 5$\mu=\sqrt{3}$ વક્રીભવનાંક ધરાવતા ધન કાચના ગોળા પર $60^{\circ}$ ના આપાતકોણ પ્રકારનું કિરણ દાખલ થાય છે. બીજી સપાટી પર કિરણનુંપરાવર્તન અને વક્રીભવન થાય છે બીજી સપાટી આગળ પરાવર્તિત અને વક્રીભૂત કિરણ વચ્ચેનો ખૂણોView Solution
- 6View Solutionશ્રી.સી.વી.રામન ને પ્રકાશની કઇ ધટના માટે નોબલ આપવામાં આવ્યું હતું?
- 7વક્રિભવન પ્રકારના ખગોલીય ટેલીસ્કોપની સામાન્ય ગોઠવણીમાં ઓબ્જેક્ટિવ અને આઈપીપ (નેત્રકાચ) વચ્ચેનું અંતર $30 \,cm$ છે. જ્યારે ટેલીસ્કોપની કોણીય મોટવણી $2$ હોય તો ઓબ્જેક્ટિવની કેન્દ્રલંબાઈ ........... $cm$ થશે.View Solution
- 8પાત્રમાં પ્રવાહી $120\,mm$ ઊંચાઇ સુધી ભરેલ છે.તેમાં રહેલ સોય $80\,mm$ ઊંડાઇ પર દેખાતી હોય,તો પ્રવાહીનો વક્રીભવનાંક કેટલો હશે?View Solution
- 9$6\,D$ અને $- 2 \,D$ પાવરના બે લેન્સને જોડીને એક લેન્સ બનાવવામાં આવે છે. તો લેન્સની કેન્દ્રલંબાઈ ......છે.View Solution
- 10બરફના ઘનની અંદર એક પરપોટો રહેલો છે. પરપોટાને એક બાજુથી જોતા તેનું અંતર $12\,cm$ દેખાય છે. જ્યારે સામેની બાજુએથી જોવા આવે, ત્યારે તેનું દેખાતું અંતર $4\,cm$ છે. જો બરફના ધનની બાજુ $24\,cm$ હોય તો બરફના ઘનનો વક્રીભવનાંક ........ છે.View Solution
