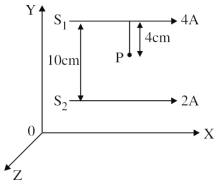
અનુક્રમે $4\,A$ અને $2\,A$ પ્રવાહ ધરાવતા બેેે લાંબા સમાંતર વાહકો $S _{1}$ અને $S _{2}$ ને $10 \,cm$ અંતરે છૂટા રાખવામાં આવ્યા છે. વાહકોને $x$-અક્ષની દિશામાં $X-Y$ સમતલમાં રાખવામાં ધરાવતો એક વીજભારિત કણ બિંદુ $P$ આગળથી $\vec{v}=(2 \hat{i}+3 \hat{j}) \,m / s$ ના વેગ સાથે પસાર થાય છે, જ્યાં $\hat{i}$ અને $\hat{j}$ અનુક્રમે $x$ અને $y$ અક્ષોની દિશામાં એકમ સદિશ છે. વિદ્યુતભારીત કણ પર લાગતું બળ $4 \pi \times 10^{-5}(-x \hat{i}+2 \hat{j}) \,N$ છે. $x$ નું મૂલ્ય ........... થશે.

JEE MAIN 2022, Diffcult
c
\(B _{ net }= B _{1}- B _{2}=\frac{\mu_{0} \times 4}{2 \pi[.04]}-\frac{\mu_{0} \times 2}{2 \pi[.06]}\)
\(B _{ net }= B _{1}- B _{2}=\frac{\mu_{0} \times 4}{2 \pi[.04]}-\frac{\mu_{0} \times 2}{2 \pi[.06]}\)
\(\overrightarrow{ B }_{\text {met }}=\frac{\mu_{0}}{2 \pi}\left[\frac{200}{3}\right](-\hat{ k })\)
\(\overrightarrow{ F }= q [\overrightarrow{ v } \times \overrightarrow{ B }]\)
\(=[3 \pi]\left[(2 \hat{ i }+3 \hat{ j }) \times\left(\frac{\mu_{0}}{2 \pi}\right)\left(\frac{200}{3}\right)-\hat{ k }\right]\)
\(=3 \pi \times \frac{\mu_{0}}{2 \pi}\left(\frac{200}{3}\right)[2 \times \hat{j}-3(\hat{i})]\)
\(=\left(4 \pi \times 10^{-7}\right)(100)(-3 \hat{i}+2 \hat{j})\)
\(=4 \pi \times 10^{-5} \times[-3 \hat{i}+2 \hat{j}]\)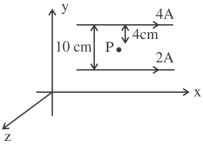
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
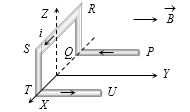
- 1ચુંબકીયક્ષેત્ર ઘન $ Y\,-$ દિશામાં છે.તાર $PQRSTU $ માં $ i$ પ્રવાહ પસાર થાય છે.તેની દરેક બાજુની લંબાઇ $ L$ છે.તેના પર કેટલું બળ લાગશે?View Solution
- 2View Solutionનિયમિત વેગ ધરાવતા એક ઈલક્ટ્રોક પ્રવાહ ધરાવતા લાંબા સોલેનોઈડની અંદર તેની અક્ષની દિશામાં પ્રક્ષિપ્ત કરવામાં આવે છે. તો . . . . . . .
- 3તારમાં $ i $ પ્રવાહ ઘન $X-$ દિશામા પસાર થાય છે.ચુંબકીયક્ષેત્ર $\overrightarrow B = {B_0}$ ($\hat i + \hat j + \hat k)$ $T$ છે.તો તેના પર કેટલું બળ લાગશે?View Solution
- 4$i$ પ્રવાહવાળા $d\vec l$ લંબાઇના ખંડથી $\vec r$ અંતરે ચુંબકીયક્ષેત્ર $d\overrightarrow B$ કેટલું થાય?View Solution
- 5આયનિય હાઈડ્રોજન પરમાણુઓ અને $\alpha -$કણો સમાન વેગમાનથી અચળ ચુંબકીય ક્ષેત્ર $B$ માં લંબ રીતે પ્રવેશે છે. તેમના પથોની ત્રિજ્યાઓનો ગુણોત્તર ${r_H}:{r_\alpha }$ કેટલો હશે?View Solution
- 6$l$ લંબાઇની સમબાજુવાળી ત્રિકોણાકાર કોઇલને એક પરમેનન્ટ ચુંબકના બંને ધ્રુવો વચ્ચે લટકાવેલ છે, કે જેથી $\vec B$ એ કોઇલના સમતલમાં રહે. જો ત્રિકોણાકાર કોઇલમાં વહેતા $I$ જેટલા વિદ્યુતપ્રવાહને લીધે તેના પર લાગતું ટોર્ક $\tau$ હોય, તો ત્રિકોણાકાર કોઇલની બાજુની લંબાઈ $l$ કેટલી હશે?View Solution
- 7બે $10 \,cm$ લાંબા, $5\,A$ નો પ્રવાહ ધરાવતા, સીધા તારોને એકબીજાને સમાંતર રાખવામાં આવેલ છે. જો દરેક તાર $10^{-5} \,N$ નું બળ અનુભવતો હોય તો તારો વચ્યેનું અંતર ......... $cm$ હશે.View Solution
- 8આપ્રશ્ન માં વિધાન $I$ અને વિધાન $II$ આપવામાં આવ્યા છે. યોગ્ય વિકલ્પ પસંદ કરો.View Solution
વિધાન $I$ : એમિટરની જેમ રેન્જ વધારે તેમ અવરોધ મોટો.
વિધાન $II$ : એમિટરની રેન્જ વધારવા માટે તેને સમાંતર વધારાનો શંટ જોડવો પડે.
- 9ગેલ્વેનોમીટરના સ્કેલ માપને $25 $ સમાન વિભાગ પાડવામાં આવે છે.ગેલ્વેનોમીટરનો અવરોધ $100 \,\Omega$ છે.ગેલ્વેનોમીટરની વિધુત સંવેદિતા $ 4 × 10^{-4} \,A/div.$ છે.ગેલ્વેનોમીટર $2.5 \,volt$ માપવા માટે કેટલા .................... $ohm$ અવરોધ શ્રેણીમાં જોડવો પડે?View Solution
- 10ઇલેક્ટ્રૉનના જેટલો જ વીજભાર ધરાવતો એક કણ $0.5\, cm$ ત્રિજ્યાના વર્તુળાકાર પથ પર $0.5\,T$ ચુંબકીય ક્ષેત્રની અસર નીચે ગતિ કરે છે. જો $100\, V/m$ નું વિદ્યુત ક્ષેત્ર તેને સુરેખ પથ પર ગતિ કરાવે, તો આ કણનું દ્રવ્યમાન કેટલું હશે?View Solution
(ઇલેક્ટ્રૉનનો વિજભાર $=1.6 \times 10^{-19}\,C$)
