તારમાં $ i $ પ્રવાહ ઘન $X-$ દિશામા પસાર થાય છે.ચુંબકીયક્ષેત્ર $\overrightarrow B = {B_0}$ ($\hat i + \hat j + \hat k)$ $T$ છે.તો તેના પર કેટલું બળ લાગશે?
Medium
Download our app for free and get started
b
\(\overrightarrow F = i(\,\overrightarrow {l\,} \times \overrightarrow B )\) \(==>\) \(\overrightarrow F = i\,[l\,\hat i \times {B_0}(\hat i + \hat j + \hat k)] = {B_0}il[\hat i \times (\hat i + \hat j + \hat k)]\) \(==>\) \(\overrightarrow F = {B_0}il[\hat i \times \hat i + \hat i \times \hat j + \hat i \times \hat k]\)\( = {B_0}il[\hat k - \hat j]\)
\(\overrightarrow F = i(\,\overrightarrow {l\,} \times \overrightarrow B )\) \(==>\) \(\overrightarrow F = i\,[l\,\hat i \times {B_0}(\hat i + \hat j + \hat k)] = {B_0}il[\hat i \times (\hat i + \hat j + \hat k)]\) \(==>\) \(\overrightarrow F = {B_0}il[\hat i \times \hat i + \hat i \times \hat j + \hat i \times \hat k]\)\( = {B_0}il[\hat k - \hat j]\)
\(\{ \hat i \times \hat i = 0,\,\hat i \times \hat j = \hat k,\,\hat i \times \hat k = - \hat j\} \)
\(F = \sqrt 2 {B_0}il\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ચલિત ગૂંચળાના ગેલ્વેનોમીટરમાં $24 \Omega$ નો શંટ લગાડતા તેનું આવર્તન $25$ કાપામાંથી $5$કાપા જેટલું ધટે છે. ગેલ્વેનોમીટરના ગૂંચળાનો અવરોધ_________હશે.View Solution
- 2જો આંટાની સંખ્યા, ક્ષેત્રફળ અને $A$ ક્ષેત્રફળ અને ગૂંચળામાંથી પસર થતાં પ્રવાહને અનુક્રમે $N,A$ અને $I$ વડે દર્શાવે તો ગૂંચળાની ચુંબકીય ચાકમાત્રા કેટલી થાય?View Solution
- 3$100 \;\Omega$ અવરોધ ધરાવતું ગેલ્વેનોમીટર એ $10\; mA$ વિદ્યુતપ્રવાહ પર પૂર્ણ સ્કેલ આવર્તન આવે છે. તો શંટનું મુલ્ય કેટલો હોવો જોઈએ કે જેથી તે $100 \;mA$ વિદ્યુતપ્રવાહ માપી શકે?View Solution
- 4$R$ જેટલી સમાન ત્રિજયા ધરાવતી બે રિંંગોના સમતલ એકબીજાને લંબ હોય તેમ સમકેન્દ્રીય છે. તેમના વહેતા વિદ્યુતપ્રવાહો અનુક્રમે $I$ અને $2I$ છે. તેમના કેન્દ્ર પર પરિણામી પ્રેરિત ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
- 5View Solutionસઇક્લોટ્રોન કોને પ્રવેગિત કરવામાં વપરાય છે?
- 6$N$ આંટા ધરાવતી સ્પાયરલ કોઇલની અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ છે. તેમાંથી $I$ પ્રવાહ પસાર કરતાં કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7View Solutionઅનિયમિત આકારની લૂપમાં પ્રવાહ પસાર કરીને ચુંબકીય ક્ષેત્રમાં મૂકવાથી ..... .
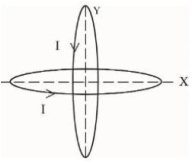
- 8બે $20\,cm$ ની સમાન ત્રિજ્યાવાળા તારો $\sqrt{2}\,A$ જેટલો વીજપ્રવાહ ધરાવે છે તેને સમતલમાં લંબરૂપે આકૃતિમાં દર્શાવ્યા પ્રમાણે મુકવામાં આવે છે. વર્તુળાકાર તારોના કેન્દ્રમાં પરિણામી ચુંબકીય ક્ષેત્ર $.......\times 10^{-8}\,T$છે.View Solution
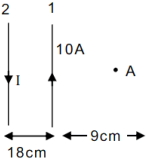
- 9બે અનંત લંબાઈના તારમાંથી પ્રવાહ પસાર થાય છે, $A$ બિંદુ આગળ ચુંબકીયક્ષેત્ર શૂન્ય હોય તો પ્રવાહ $I=.....$ ($A$ માં)View Solution
- 10હાઇડ્રોજન પરમાણુમાં ઈલેકટ્રોન તેના ન્યુકિલયસને ફરતે $6.76 \times 10^6\,ms ^{-1}$ ઝડપથી $0.52 \mathring A$ ત્રિજ્યાની કક્ષામાં પરિભ્રમણ કરે છે. હાઈડ્રોજન પરમાણુના ન્યુકિલયસમા ઉદભવતું ચુંબકીય ક્ષેત્ર ..... $T$ છે.View Solution