બે અનુક્રમે $m_1 $ અને $m_2$ દળના ગોળા $A$ અને $B$ અથડાય છે. $A$ ગોળો શરૂઆતમાં સ્થિર અને $B$ ગોળો $ v$ વેગથી $x-$ અક્ષની દિશામાં ગતિ કરે છે. અથડામણ પછી $B$ ગોળોનો વેગ $\frac {v}{2}$ મૂળ વેગની દિશાને લંબ દિશામાં છે. $A$ ગોળો અથડામણ પછી કઈ દિશામાં ગતિ કરશે?
AIPMT 2012, Diffcult
d
\(\begin{array}{l}
According\,to\,law\,of\,conservation\,of\\
linerar\,momentum\,along\,x - axis,\,we\,get\\
{m_1} \times 0 + {m_2} \times v = {m_1}v'\cos \theta \\
{m_2}v = {m_1}v'\cos \theta \\
or\,\cos \theta = \frac{{{m_2}v}}{{{m_1}v'}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
According\,to\,law\,of\,conservation\,of\,\\
linear\,momentum\,along\,y - axis,\,we\\
get
\end{array}\)
\(\begin{array}{l}
According\,to\,law\,of\,conservation\,of\\
linerar\,momentum\,along\,x - axis,\,we\,get\\
{m_1} \times 0 + {m_2} \times v = {m_1}v'\cos \theta \\
{m_2}v = {m_1}v'\cos \theta \\
or\,\cos \theta = \frac{{{m_2}v}}{{{m_1}v'}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
According\,to\,law\,of\,conservation\,of\,\\
linear\,momentum\,along\,y - axis,\,we\\
get
\end{array}\)
\(\begin{array}{l}
{m_1} \times 0 + {m_2} \times 0 = {m_1}v'\sin \theta + {m_2}\frac{v}{2} - {m_2}\frac{v}{2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {m_1}v'\sin \theta \\
\sin \theta = - \frac{{{m_2}v}}{{2{m_1}v'}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\\
Divide\,\left( {ii} \right)\,by\,\left( i \right),\,we\,get\\
\tan \theta = - \frac{1}{2}\,or\,\theta = {\tan ^{ - 1}}\left( { - \frac{1}{2}} \right)\,to\,the\,x - axis
\end{array}\)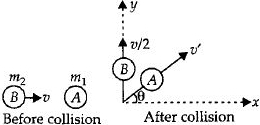
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$0.3\,kg\,m/s$ રેખીય વેગમાન ધરાવતા રેખીય ગતિ કરતાં $5\,g$ દળના પદાર્થે $5\,s$ માં કાપેલ અંતર $..........\,m$ હશે.View Solution
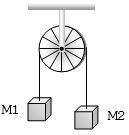
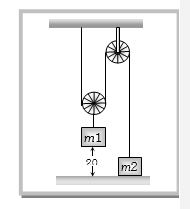
- 2વજનરહિત અને ઘર્ષણરહિત ગરગડીમાંથી પસાર થઈને વજનહીન તાર સાથે ${m_1}$ અને ${m_2}$ (ઊભી) દળના બે બ્લોકને જોડેલા છે. જો તંત્રનો પ્રવેગ $\left( {\frac{g}{8}} \right)$ હોય, તો દળનો ગુણોત્તર કેટલો હશે?View Solution
- 3કોઈ $m$ દળના કણ પર પ્રયોગમુલક નિયમ પ્રમાણે બળ $F = \frac{R}{{{t^2}}}\,v(t)$ લગાવવામાં આવે છે. ગતિની શરુઆતની સ્થિર સ્થિતિ થી પ્રાયોગિક રીતે આ નિયમ ની કસોટી કરવી હોય તો તેના માટે ..... નો વક્ર દોરવો એ ઉત્તમ રસ્તો છે.View Solution
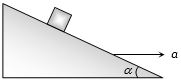
- 4બ્લોકને ઘર્ષણરહિત ઢાળ પર સ્થિર રાખવા માટે $a=$View Solution
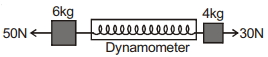
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ડાયનામોમીટર $D$ ને $6 \,kg$ અને $4 \,kg$ ઘળનાં બે બ્લોક્સ સાથે જોડેલ છે. ડાયનામોમીટરનું વાંચન .......... $N$ છે.View Solution
- 6જો $ m_1 = 4m_2$ હોય,તો $m_2 $ નો પ્રવેગ કેટલો થાય? $m_1 $ નો પ્રવેગ $a$ છે.View Solution
- 7$100\, g$ દળ ધરાવતી વસ્તુ પર $(10 \hat{i}+5 \hat{j}) N$ જેટલું બળ લાગે છે. વિરામ સ્થિતિમાંથી શરૂ કરીને $t =2 s$ એ વસ્તુનું સ્થન $( a \hat{i}+ b \hat{j}) m$ થાય છે. $\frac{ a }{ b }$ નું મૂલ્ય..........મળે છેView Solution
- 8બૉલને જમીન પરથી શિરોલંબ દિશામાં ( $+z-$ અક્ષ) ફેકવામાં આવે છે, તો નીચેનામાથી વેગમાન વિરુદ્ધ ઊંચાઈનો આલેખ કયો સાચો પડે?View Solution
- 9$10 \,kg$ દળ ધરાવતી બંદૂકમાંથી $4$ ગોળી પ્રતિ સેકન્ડે છોડવામાં આવે છે.ગોળીનું દળ $20 \,g$ અને તેનો વેગ $300\, m / s$ છે.તો ગોળી છોડતી વખતે બંદૂકને પકડી રાખવામાં કેટલા બળની ($N$ માં) જરૂર પડે?View Solution
- 10$4 \,{kg}$ દળવાળી બંદૂકમાંથી $4\,g$ દળવાળી ગોળી છોડવામાં આવે છે. જો ગોળી $50\, {ms}^{-1}$ ની ઝડપ સાથે આગળ વધે છે, તો બંદૂકને આપવામાં આવતો આઘાત અને બંદૂકના પાછળના ભાગનો વેગ કેટલો હશે?View Solution
