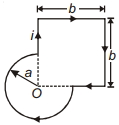
બે અર્ધવર્તુળાકાર $R$ ત્રિજયાના ભાગની બનેલ એક પ્રવાહધારીત લૂપનો એક ભાગ $xy$ સમતલમાં અને બીજો ભાગ $xz$ સમતલમાં છે. જો તેમાંથી $I$ પ્રવાહ પસાર થાય છે. બે અર્ધવર્તુળાકાર ભાગના કારણે તેમના સામાન્ય કેન્દ્ર પર પરિણામી ચુંબકીયક્ષેત્ર કેટલું થાય?
AIPMT 2010, Medium
a
The loop mentioned in the question must look like one as shown in the figure.
The loop mentioned in the question must look like one as shown in the figure.
Magnetic field at the centre due to semicircular loop lying in \(x-y\) plane, \(B_{x y}=\frac{1}{2}\left(\frac{\mu_{0} i}{2 R}\right) \quad\) negative \(z\) direction.
Similarly field due to loop in \(x-z\) plane,
\(B_{x z}=\frac{1}{2}\left(\frac{\mu_{0} i}{2 R}\right)\) in negative \(y\) direction.
\(\therefore\) Magnitude of resultant magnetic field,
\(B =\sqrt{B_{x y}^{2}+B_{x z}^{2}}=\sqrt{\left(\frac{\mu_{0} i}{4 R}\right)^{2}+\left(\frac{\mu_{0} i}{4 R}\right)^{2}}\)
\(=\frac{\mu_{0} i}{4 R} \sqrt{2}=\frac{\mu_{0} i}{2 \sqrt{2} R}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પ્રોટોન એકબીજાને સમાંતર $v=4.5 \times 10^{5} \,m / s$ ના વેગથી ગતિ કરે છે. તેમની વચ્ચે લાગતા વિદ્યુત અને ચુંબકીય બળનો ગુણોતર કેટલો થાય?View Solution
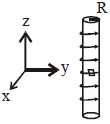
- 2$R$ ત્રિજ્યા ધરાવતા લાંબા સોલેનોઈડની અંદર અક્ષ પર એક ઇલેક્ટ્રોન ગન મૂકવામાં આવેલ છે. સોલેનોઈડમાં એકમ લંબાઈ દીઠ આંટાની સંખ્યા $n$ અને વહેતો પ્રવાહ $I$ છે.ઇલેક્ટ્રોન ગન સોલેનોઈડમાં ત્રિજયવર્તી દિશામાં $v$ વેગથી ઇલેક્ટ્રોન છોડે છે. જો ઇલેક્ટ્રોન સોલેનોઈડની સપાટી પર પહોચે નહીં તે માટે તેનો મહત્તમ વેગ $v$ કેટલો હોવો જોઈએ?View Solution
- 3$q$ વિદ્યુતભાર અને $m$ દળ ધરાવતો કણ $x-$ અક્ષની દિશામાં $v$ વેગથી ગતિ કરે છે.તો કઇ આકૃતિમાં ઇલેકટ્રોન વિચલન થયા વગર પસાર થશે?View Solution
- 4$R$ ત્રિજયાની પ્રવાહધારિત રીંગની અક્ષ પર કેટલા અંતરે ચુંબકીયક્ષેત્ર કેન્દ્ર પરના ચુંબકીયક્ષેત્ર કરતાં $ \frac{1}{8} $માં ભાગનું થાય?View Solution
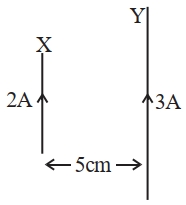
- 5$50\,cm$ લંબાઈના એક તાર $X$ને અને $2\; A$ પ્રવાહ ધરાવતા $5\,m$ લાંબા તાર $Y$ ને સમાંતર મૂકવામાં આવેલ છે. તાર માં $3\; A$ પ્રવાહ વહે છે. બે તારો વચ્ચેનું અંતર $5\,cm$ અને તેમાં સમાન દિશામાં પ્રવાહ વહે છે. $Y$ તાર ઉપર લાગતું બળ $..........$ હશે.View Solution
- 6View Solutionસમાન લંબાઇના તારમાંથી બનાવેલ વર્તુળ અને ચોરસના કેન્દ્ર પર ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?
- 7જેમાં $I$ જેટલો વિદ્યુતપ્રવાહ વહે છે તેવા એક સુવાહક તારને $N$ આંટા ધરાવતા વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે ત્યાર બાદ તેને $n$ આંટા ધરાવતાં વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે. બંને ગૂંચળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર ગણવામાં આવે છે. પ્રથમ કિસ્સામાં અને બીજા કિસ્સામાં મળતા ચુંબકીય ક્ષેત્રનો ગુણોતર $.............$ થશે.View Solution
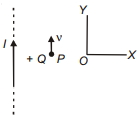
- 8દર્શાવ્યા પ્રમાણે $I$ વિદ્યુતપ્રવાહ ધરાવતા ખૂબ જ લાંબા સીધા તારને સમાંતર વિદ્યુતભાર $Q$ ગતિ કરે છે. વિદ્યુતભાર પર લાગતું બળ કઈ દિશામાં છે ?View Solution
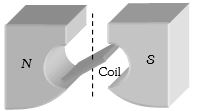
- 9$A$ ક્ષેત્રફળ અને $ i$ પ્રવાહધારિત $n $ આંટાવાળી કોઇલનું સમતલ ચુંબકીયક્ષેત્ર સાથે $ \theta $ ખૂણો બનાવે છે.તો કોઇલ પર કેટલું ટોર્ક લાગશે?View Solution
- 10વિદ્યુતપ્રવાહ $i$ સાથેની રીંગ જેનો આકાર આાકૃતિમાં દર્શાવેલ છે. તેના બિંદુ $O$ પાસે ચુંબકીયક્ષેત્રની તીવ્રતા કેટલી છે ?View Solution