બે પ્રોટોન એકબીજાને સમાંતર $v=4.5 \times 10^{5} \,m / s$ ના વેગથી ગતિ કરે છે. તેમની વચ્ચે લાગતા વિદ્યુત અને ચુંબકીય બળનો ગુણોતર કેટલો થાય?
AIIMS 2019, Diffcult
Download our app for free and get started
a
The expression for electric force is given by,
The expression for electric force is given by,
\(F_{ E }=\frac{k e^{2}}{r^{2}}\) \(...(I)\)
The expression for magnetic force is given by,
\(F_{ M }=\frac{e^{2} V^{2} \mu_{0}}{4 \pi r^{2}}\) \(...(II)\)
Divide equation \((I)\) and \((I).\)
\(\frac{F_{ E }}{F_{ M }}=\frac{\frac{k e^{2}}{r^{2}}}{\frac{e^{2} V^{2} \mu_{0}}{4 \pi r^{2}}}\)
\(=\frac{k 4 \pi}{V^{2} \mu_{0}}\) \(...(III)\)
Substitute \(9 \times 10^9\) for \(k, 4.5 \times 10^{5} m / s\) for \(V\) and \(4 \pi \times 10^{-7}\) for \(\mu_\circ\) in equation \((III).\)
\(\frac{F_{ E }}{F_{ M }}=\frac{9 \times 10^9 \times 4 \pi}{\left(4.5 \times 10^{5} m / s \right)^{2} 4 \pi \times 10^{-7}}\)
\(=4.4 \times 10^{5}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
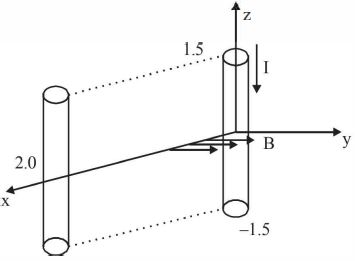
- 1આકૃતિમાં બતાવ્યા પ્રમાણે એક સુવાહક કે જે $Z-$ અક્ષને સમાંતર $-1.5$$ \le Z < 1.5\,m$ વચ્ચે રહેલ છે,જેમાંથી $ - {\hat a_z}$ દિશામાં $10.0$ $A$ નો અચળ પ્રવાહ વહે છે.આપેલ સૂત્ર $\vec B$ $=$ $3.0 \times 10^{-4}$ $e^{-0.2x}$ ${\hat a_y}\,T$ માટે સુવાહકને અચળ ઝડપે $5 \times 10^{-3} $ $ s$ સમય ગાળામાં $x=2.0$ $m$ $,y=0$ $m$ સ્થાને લઇ જવા જરૂરી કાર્ય-દર .......$W$ માં શોધો.આ ગતિ $X-$ અક્ષને સમાંતર છે,એવું ધારો.View Solution
- 2એક લાંબી, સુરેખ અને પાતળી દિવાલવાળી પાઇપમાંથી વિદ્યુતપ્રવાહ $I$ વહે છે. તો નીચેનામાંથી ક્યું વિધાન સાયું છે?View Solution
- 3$L$ લંબાઇના તારમાંથી $i$ પ્રવાહ પસાર થાય છે.તો મધ્યબિંદુથી $ \frac{L}{4} $ અંતરે ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
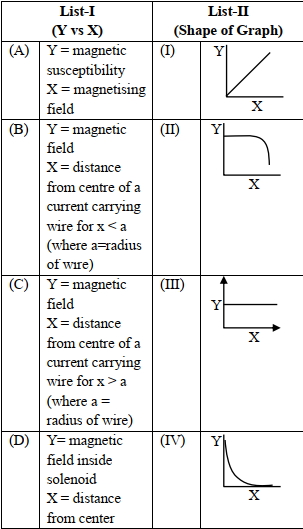
- 4લિસ્ટ -$I$ ને લિસ્ટ-$II$ સાથે જોડો. આપેલ પૈકી ક્યો વિકલ્પ સાચો છે .View Solution
- 5ગુણાકારView Solution
$\overrightarrow{\mathrm{F}} =\mathrm{q}(\vec{v} \times \overrightarrow{\mathrm{B}})$
$=\mathrm{q} \vec{v} \times\left(\mathrm{B} \hat{i}+\mathrm{B} \hat{j}+\mathrm{B}_{0} \hat{k}\right)$
માં $\mathrm{q}=1,$ $\vec{v}=2 \hat{i}+4 \hat{j}+6 \hat{k}$ અને બળ $\overrightarrow{\mathrm{F}}=4 \hat{i}-20 \hat{j}+12 \hat{k}$
$\vec{B}$નું સંપૂર્ણ સમીકરણ શું હશે?
- 6જ્યારે વિદ્યુતભારિત કણ $\overrightarrow{v}$ વેગથી $\overrightarrow{B}$ જેટલા ચુંબકીયક્ષેત્રમાં ગતિ કરે ત્યારે તેના પર લાગતું બળ શૂન્ય નથી, તો તે બતાવે છે કેView Solution
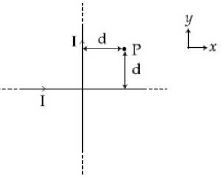
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે $xy$ સમતલમાં બે લાંબા અને અવાહક તારને $90^o$ ના ખૂણે મૂકેલા છે.આ તારમાંથી સમાન મૂલ્યનો પ્રવાહ $I$ આકૃતિમાં દર્શાવ્યા પ્રમાણેની દિશામાં પસાર થાય છે. $P$ બિંદુ આગળ કુલ ચુંબકીય ક્ષેત્ર કેટલું થશે?View Solution
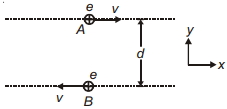
- 8બે પ્રોટોન $A$ અને $B, x$-અક્ષને સમાંતર, પરસ્પર વિરુદ્ધ દિશામાં, સમાન ઝડપે $V$ સાથે ગતિ કરે છે. દર્શાવેલ ક્ષણે, પ્રોટોન $A$ પર લાગતા ચુંબકીય બળ અને વિદ્યુતબળનો ગુણોત્તર કેટલો છે ? ($c =$ શૂન્યાવકાશમાં પ્રકાશની ઝડ૫)View Solution
- 9$4 \times 10^{5}\, ms ^{-1}$ ના વેગથી ગતિ કરતું એક પ્રોટોનનું કિરણપુંજ $0.3\, T$ જેટલા ચુંબકીયક્ષેત્રમાં ક્ષેત્રને $60^o$ ના ખૂણે પ્રવેશે છે. જેના કારણે બનતા હેલિકલ પથની પિચ(પેચઅંતર) કેટલા $cm$ હશે?View Solution
(પ્રોટોનનું દળ $=1.67 \times 10^{-27}\, kg$, પ્રોટોનનો વિજભાર $=1.69 \times 10^{-19}\,C$)
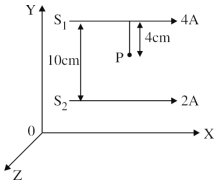
- 10અનુક્રમે $4\,A$ અને $2\,A$ પ્રવાહ ધરાવતા બેેે લાંબા સમાંતર વાહકો $S _{1}$ અને $S _{2}$ ને $10 \,cm$ અંતરે છૂટા રાખવામાં આવ્યા છે. વાહકોને $x$-અક્ષની દિશામાં $X-Y$ સમતલમાં રાખવામાં ધરાવતો એક વીજભારિત કણ બિંદુ $P$ આગળથી $\vec{v}=(2 \hat{i}+3 \hat{j}) \,m / s$ ના વેગ સાથે પસાર થાય છે, જ્યાં $\hat{i}$ અને $\hat{j}$ અનુક્રમે $x$ અને $y$ અક્ષોની દિશામાં એકમ સદિશ છે. વિદ્યુતભારીત કણ પર લાગતું બળ $4 \pi \times 10^{-5}(-x \hat{i}+2 \hat{j}) \,N$ છે. $x$ નું મૂલ્ય ........... થશે.View Solution
