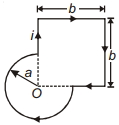
વિદ્યુતપ્રવાહ $i$ સાથેની રીંગ જેનો આકાર આાકૃતિમાં દર્શાવેલ છે. તેના બિંદુ $O$ પાસે ચુંબકીયક્ષેત્રની તીવ્રતા કેટલી છે ?

Medium
a
(a)
(a)
\(\bar{B}\) due to square part :-
\(\vec{B}\) due to side \(O A\) and \(O C\) will be zero at point \(O\)
\(\bar{B}\) due to side \(A B\) and \(B C\) will be equal so
\(\bar{B}_1=2\left[\frac{\mu_0 i}{4 \pi b}\left(\sin 45^{\circ}+0\right)\right]=\frac{\mu_0 i}{2 \sqrt{2} \pi b} \otimes\)
\(\vec{B}\) due to circular part
\(\bar{B}_2=\frac{\mu_0 i}{2 a}\left[\frac{\left(\frac{3 \pi}{2}\right)}{2 \pi}\right]=\frac{3 \mu_0 i}{8 a} \otimes\)
\(\overline{B_{\text {net }}}=\overline{B_1}+\bar{B}_2=\mu_0 i\left[\frac{3}{8 a}+\frac{1}{2 \sqrt{2} \pi b}\right]=\frac{\mu_0 i}{4 \pi}\left[\frac{3 \pi}{2 a}+\frac{\sqrt{2}}{b}\right]\)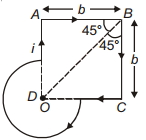
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$0.01\,{m^2}$ ક્ષેત્રફળ ધરાવતા વર્તુળાકાર લૂપમાંથી $10\;A$ નો પ્રવાહ વહે છે, જેને $0.1\,T$ ચુંબકીયક્ષેત્રમાં લંબરૂપે ગોઠવેલ છે. લૂપ પર લાગતું ટોર્ક ($N-m$ માં) કેટલું હશે?View Solution
- 2એક ઇલેકટ્રોન $r$ ત્રિજયાની વર્તુળાકાર કક્ષામાં એક સેકન્ડમાં $n$ પરિભ્રમણ કરે છે. તેના કેન્દ્ર પર કેટલું ચુંબકીયક્ષેત્ર ઉત્પન્ન થશે?View Solution
- 3અચળ, સમાન અને પરસ્પર લંબ એવાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }$ અને યુંબકીય ક્ષેત્ $\overrightarrow{ B }$ ના બનેલા પ્રદેશમાં એક વિદ્યુતભારિત કણ $\overrightarrow{v}$ વેગથી $\overrightarrow{ E }$ અને $\overrightarrow{ B }$ બંનેની લંબ દિશામાંથી પ્રવેશે છે અને વેગમાં કોઈપણ પ્રકારના ફેરફાર વિના બહાર આવે છે. કણ પરનો વિદ્યુતભાર $q$ હોય, તો ....View Solution
- 4કોઈ એક ક્ષેત્રમાં સ્થિત વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્ર પ્રવર્તે છે.ચુંબકીયક્ષેત્ર $\vec B = {B_0}\left( {\hat i + 2\hat j - 4\hat k} \right)$ મુજબ આપવામાં આવે છે. જો એક વિજભાર આ ક્ષેત્રમાં $\vec v = {v_0}\left( {3\hat i - \hat j + 2\hat k} \right)$ ના વેગથી ગતિ કરતો હોય ત્યારે કોઈ બળ અનુભવતો ના હોય તો $SI$ એકમમાં વિદ્યુતક્ષેત્ર કેટલું હશે?View Solution
- 5$2000 $ આંટા અને $1.5 \times 10^{-4}\ m^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો સોલેનોઇડ $2\ A $ પ્રવાહનું વહન કરે છે. સોલેનોઇડને કેન્દ્ર પર અને તેની લંબાઈને લંબ દોરી વડે લટકાવેલ છે કે જેથી તે $5 \times 10^{-2} \;T $ ચુંબકીયક્ષેત્રમાં તેની અક્ષ સાથે $ 30^o$ ના ખૂણે સમક્ષિતિજ સમતલમાં ફરી શકે. સોલેનોઇડ પર લાગતું ટોર્ક કેટલું હશે?View Solution
- 6બે સમાંતર રહેલા પ્રવાહધારિત તાર વચ્ચેનું અંતર $b$ છે.તો એક તાર દ્વારા બીજા તારના એકમ લંબાઇ દીઠ કેટલું બળ લાગશે?View Solution
- 7એમીટરનો અવરોઘ $13\,\Omega $ છે અને તેનો સ્કેલ $100\,A$ સુધીના પ્રવાહ માપી શકે છે. વધારાના શંટને આ એમીટર સાથે જોડવામાં આવ્યા પછી આ એમીટર દ્વારા $ 750 \,A$ સુધીના પ્રવાહોને માપવાનું શક્ય બને છે. તો શંટ અવરોઘનું મૂલ્ય કેટલું હશે?View Solution
- 8જેમાં $I$ જેટલો વિદ્યુતપ્રવાહ વહે છે તેવા એક સુવાહક તારને $N$ આંટા ધરાવતા વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે ત્યાર બાદ તેને $n$ આંટા ધરાવતાં વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે. બંને ગૂંચળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર ગણવામાં આવે છે. પ્રથમ કિસ્સામાં અને બીજા કિસ્સામાં મળતા ચુંબકીય ક્ષેત્રનો ગુણોતર $.............$ થશે.View Solution
- 9$4 \,{amu}$ અને $16\, amu$ દળ ધરાવતા બે આયન પરના વિદ્યુતભાર અનુક્રમે $+2 {e}$ અને $+3 {e}$ છે. આ આયનો સતત લંબરૂપ ચુંબકીય ક્ષેત્ર ધરાવતા પ્રદેશમાંથી પસાર થાય છે. જો બંને આયનની ગતિઉર્જા સમાન હોય તો ....View Solution
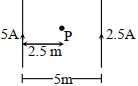
- 10આપેલી આકૃતિમાં રહેલ બિંદુ $P$ પરનું ચુંબકીય ક્ષેત્ર કેટલું થશે?View Solution