બે અવાહક પ્લેટોને સમાન રીતે વિદ્યુતભારીત કરેલી છે. તેમની વચ્ચેનો વિદ્યુત સ્થિતિમાનો તફાવત $V _{1}- V _{2}=20\; V$ (જ્યાં પ્લેટ$-2$ વધારે સ્થિતિમાને) છે. બે પ્લેટો વચ્ચેનું અંતર $0.1\; m$ છે અને તે અનંત સુધી વિસ્તરેલી છે. પ્લેટ$-1$ ની અંદરની સપાટી પરથી એક ઈલેક્ટ્રોન સ્થિર સ્થિતિમાંથી મુક્ત થાય, તો જ્યારે તે પ્લેટ$-2$ ને અથડાય ત્યારે તેનો વેગ કેટલો હશે ?
($e=1.6 \times10^{-1}9\; C$,$m_e=9.11 \times 10^{-3}\;kg$)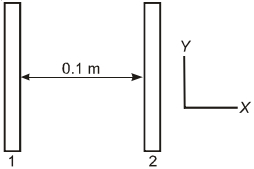
AIEEE 2006, Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
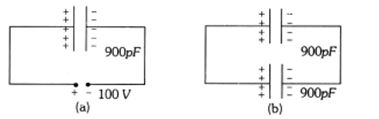
- 1આકૃતીમાં દર્શાવેલ કેપેસીટરમાં સંગ્રહીત ઉર્જા $4.5 \times 10^{-6}\ J$ છે. જો બેટરીને બીજા $900\,pF$ ના કેપેસીટર વડે બદલવામાં આવે તો તંત્રની કુલ ઉર્જા શોધો ?View Solution
- 2એક ટૂંકા વિદ્યુત દ્વિધ્રુવીયની દ્વિધ્રુવીય ચાક્માત્રા $16 \times 10^{-9}\, Cm$ છે. આ દ્વિધ્રુવીયના અક્ષ સાથે $60^{\circ}$ ખૂણો બનાવતી એક રેખા પર, આ દ્વિધ્રુવીયના કેન્દ્રથી $0.6\, m$ અંતરે રહેલ એક બિંદુ પર આ દ્વિધ્રુવીયના કારણે લાગતું વિધુતસ્થિતિમાન $.........V$ છેView Solution
$\left(\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} Nm ^{2} / C ^{2}\right)$
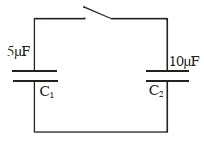
- 3$5 \,\mu F$ ના મૂલ્યના એક સંઘારકને $C _{1} 30 \,V$ ના સ્થિતિમાન થી બેટરી વડે વીજભારિત કરવામાં આવે છે. ત્યારબાદ બેટરીને દૂર કરવામાં આવે છે એ આકૃતિમાં દર્શાવ્યા અનુસાર બીજા $10 \,\mu F$ ના અવિદ્યુતભારિત સંઘારક સાથે જોડવામાં આવે છે. જ્યારે કળ બંધ હોય છે ત્યારે સંધારક વચ્ચે વીજભારનું વહન થાય છે. સંતુલન સમયે, બીજા સંઘારક $C _{2}$ પરનો વિદ્યુતભાર ........... $\mu C$ હશે.View Solution
- 4એક વિદ્યુત પરિપથમાં $1.0$ $kV$ વિદ્યુત વિભવની સામે $2$$\mu F$ કેપેસિટરોની જરૂર છે.$1$$\mu F$ ના ખૂબ જ મોટી સંખ્યામાં કેપેસિટરો છે,જે $300$ $V$ ના વિદ્યુત વિભવ કરતા વધુ વિદ્યૂત વિભવ સહિ શકતા નથી. તો આ માટે જરૂરી ઓછામાં ઓછા કેપેસિટરોની સંખ્યાView Solution
- 5પાતળી ધાતુની પટ્ટી દ્વારા બનાવેલ કેપેસીટરનું કેપેસીટન્સ $2\ \mu F$ છે જો પાતળી ધાતુની પટ્ટીઓને $0.15\, mm $ જાડાઇના પેપેર વડે ભરવામાં આવે તથા પેપરનો ડાલઇલેક્ટ્રીક અચળાંક $2.5$ તથા લંબાઇ $400 \,mm$ હોય તો પટ્ટીની લંબાઇ.....$m$View Solution
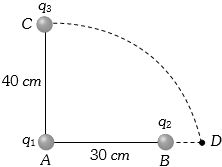
- 6આકૃતિમાં દર્શાવ્યા મુજબ be $q_1$ અને $q_2$ વિદ્યુતભાર $30\;cm$ અંતરે છે. ત્રીજો વિદ્યુતભાર $q_3$ ને $C$ થી $D$ સુધી $40 \;cm$ ત્રિજ્યાના વર્તુળની ચાપ પર લઇ જવામાં આવે છે. તંત્રની સ્થિતિઊર્જામા $\frac{{{q_3}}}{{4\pi {\varepsilon _0}}}k$ ફેરફાર થાય તો, $k=$View Solution
- 7View Solutionસમાંતર પ્લેટ કેપેસીટન્સમાં પ્લેટને અલગ કરવા માટે કરવું પડતું કાર્ય મેળવો.
- 8આકૃતિમાં દર્શાવ્યા મુજબ ત્રણ ચાર્જને $x=-a, x=0$ અને $x=a$, એમ $x$ અક્ષ પરરાખવામાં આવેલ છે. આ પ્રણાલીની સ્થિતિઊર્જા કેટલી થશે?View Solution
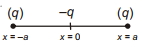
- 9$r$ અંતરે આવેલા સમાન વિદ્યુતભારિત ગોળાની બહારની બાજુએ વિદ્યુત સ્થિતિમાન ($a$ = ગોળાની ત્રિજ્યા) ........View Solution
- 10$P(x, y)$ બિંદુએ વિધુતસ્થિતિમાન $V = axy$ હોય તો, $P$ થી $r$ અંતરે વિદ્યુતક્ષેત્ર કોના સપ્રમાણમાં હોય?View Solution