બે બિંદુગત વિદ્યુતભારો $e$ અને $3 e$ ને $r$ અંતરે મૂકવામાં આવ્યા છે. વિદ્યુતભારથી કેટલા અંતરે વિદ્યુતક્ષેત્ર તીવ્રતા શૂન્ય હશે ?
Medium
Download our app for free and get started
b
(b)
(b)
Net electric field at \(P\) is zero then
\(O=E_1-E_2\)
\(E_1=E_2\)
\(\frac{k e}{x^2}=\frac{k 3 e}{(r-x)^2}\)
so, \(\frac{1}{x}=\frac{\sqrt{3}}{r-x}\)
\(r-x=\sqrt{3} x\)
\(r=x[1+\sqrt{3}]\)
\(x=\frac{r}{(1+\sqrt{3})}\)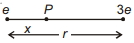
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
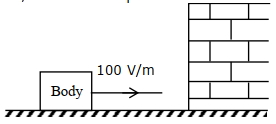
- 1$8\,\mu {C} / {g}$ વિશિષ્ટ વિદ્યુતભાર ધરાવતો એક પદાર્થ આકૃતિમાં દર્શાવ્યા પ્રમાણે ઘર્ષણરહિત સમતલ પર દીવાલથી $10\, {cm}$ અંતરે છે. તેના પર દીવાલ તરફ $100 \,{V} / {m}$ જેટલું એકસમાન વિદ્યુતક્ષેત્ર લગાવતા તે દીવાલ તરફ ગતિ કરે છે. જો પદાર્થ દીવાલ સાથે સંપૂર્ણ સ્થિતિસ્થાપક અથડામણ કરે તો આ ગતિનો આવર્તકાળ ($sec$ માં) કેટલો થાય?View Solution
- 2$+2\,C$ અને $+6\,C $ વચ્ચે લાગતું અપાકષૅણ બળ $12\,N$ છે,હવે જો $-2\,C$ વિદ્યુતભાર બંનેમાં ઉમેરતાં તેના વચ્ચે કેટલું બળ લાગે?View Solution
- 3$R$ ત્રિજ્યાનો અવાહક ધન ગોળો સમાન રીતે વિદ્યુતભારીત થયેલો છે. તેના કેન્દ્રથી $r$ અંતરે આવેલ ગોળાને લીધે વિદ્યુતક્ષેત્રનું મૂલ્ય ........ છે.View Solution
$(1)\, r$ ના વધારા સાથે વધે છે $r < R \,$
$(2)\, r$ ના વધારા સાથે ઘટશે $0 < r <$ $\infty$
$(3)\, r$ ના વધારા સાથે ઘટશે $R < r < \infty \,$
$(4)\, r = R$ આગળ તે સતત છે.
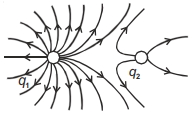
- 4View Solutionઆકૃતીમાં વિદ્યુતભાર રચનાને કારણે વિદ્યુતક્ષેત્ર રેખાઓ દર્શાવેલ છે. આ પરથી આપણો કહીં શકીએે કે
- 5બે બિંદુવત $+ 2$ $\mu $$C$ અને $+ 6$ $\mu $$C$ ના વિદ્યુતભારો એકબીજાને $12\, N$ બળથી અપાકર્ષે છે. જો દરેકમાં $- 4$ $\mu $$C$ નો વિદ્યુતભાર ઉમેરવામાં આવે તો બળ ...... હશે.View Solution
- 6$-q$ વિદ્યુતભાર અને $m$ દળ ધરાવતો એક કણ અનંત લંબાઈ અને $+\lambda$ જેટલી રેખીય વિદ્યુતભાર ધનતા ધરાવતા રેખીય વિદ્યુતભારને ફરતે $r$ ત્રિજ્યા ધરાવતા વર્તુળ ઉપર ગતિ કરે છે. આવર્તકાળ___________વડે આપી શકાય.View Solution
( $k$ ને કુલંબના અચળાંક તરીકે લો.)
- 7$M$ દળ અને $q$ વિજભાર $k$ દળ ધરાવતી સ્પ્રિંગ સાથે જોડાયેલ છે. $x = 0$ ને સમતોલન સ્થાન રાખીને તે $x-$દિશામાં $A$ કંપવિસ્તારથી દોલનો કરે છે,$x-$દિશામાં $E$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્તે છે. તો નીચેનામાંથી કયું વિધાન સાચું પડે?View Solution
- 8વિદ્યુત દ્રીધ્રુવીને લીધે વિષુવરેખીય સમતલ પર તેના કેન્દ્રથી દૂરના અંતર $(r)$ આગળ વિદ્યુત ક્ષેત્ર અંતર સાથે .......... મુજબ બદલાય છે.View Solution
- 9$1$ ઇલેક્ટ્રોન જેટલો વિદ્યુતભાર તથા $10^{-5}\, cm$ ત્રિજ્યા ધરાવતા પાણીના ટીપાને હવામાં મુક્ત રાખવા માટે જરૂરી વિદ્યુત ક્ષેત્રની તિવ્રતા...View Solution
- 10$R$ ત્રિજયા ધરાવતા વિદ્યુતભારીત વાહક ગોળીય કવચના કેન્દ્રથી $\frac{{3R}}{2}$ અંતરે વિદ્યુતક્ષેત્ર $E\; V/m$ છે. તેના કેન્દ્રથી $\frac{R}{2}$ અંતરે વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution