બે ડ્યુટેરોન એક બીજા તરફ સમાન ઝડપથી ગતિ કરે છે. તેમની વચ્ચેનું સૌથી નજીકત્તમ અંતર $2\, fm$ હોય, તો તેમની પ્રારંભિક ગતિ ઊર્જા કેટલા .....$MeV$ હોવી જોઈએ?
Medium
Download our app for free and get started
a
\(P.E.\) માં વધારો \(=K.E. \) માં ઘટાડો
\(P.E.\) માં વધારો \(=K.E. \) માં ઘટાડો
\(\frac{{k{q_1}{q_2}}}{r}\, = \,\,\frac{1}{2}\,\,m{v^2} + \frac{1}{2}\,m{v^2} = \,\,2\,\,(KE)\,\,\)
\(\, \Rightarrow \,\,2\,(K.E.)\,\, = \,\,\frac{{9\,\, \times \,\,{{10}^9} \times \,\,1.6\,\, \times \,\,{{10}^{ - 19}}}}{{2\,\, \times \,\,{{10}^{ - 15}}}}\,\,\,(in\,\,eV)\)
\( = \,\,\frac{{9\,\, \times \,\,{{10}^9} \times 0.8\,\, \times \,\,{{10}^{ - 19}}}}{{{{10}^{ - 15}}}}\,\, = \,\,7.2\,\, \times \,\,{10^5}\,\, = \,\,0.72\,\,MeV.\)
તેથી ગતિ ઉર્જા \( = \,\,\,\frac{{0.72}}{2}\,\, = \,\,0.36\,\,MeV\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ક્ષ કિરણ ટ્યૂબ $50 \,kV$ અને $20 \,mA$ પર કાર્ય કરે છે. ટ્યૂબના ટાર્ગેંટ પદાર્થનું દળ $1.0 \,kg $ અને $495 \,Jkg^{-1}{°}C^{-1}$ છે. એક પ્રતિશત લાગુ પાડેલ વિદ્યુત પાવરને ક્ષ કિરણોમાં રૂપાંતરિત કરવામાં આવે છે. અને બાકી રહેલી સંપૂર્ણ ઊર્જાને ટાર્ગેંટને ગરમ કરવામાં વપરાય છે, તો.....View Solution
$(1)$ એક યોગ્ય ટાર્ગેંટ પદાર્થનું ગલન તાપમાન ઉંચુ હોવું જોઈએ.
$(2)$ એક યોગ્ય ટાર્ગેંટ પદાર્થ પાસે ઓછી ઉષ્મીય વાહકતા હોવી જોઈએ.
$(3)$ ટાર્ગેંટના તાપમાનના વધારાનો સરેરાશ દર $ 2°C/s$ હોવો જોઈએ.
$(4)$ ઉત્સર્જાતા ક્ષ કિરણની ન્યૂનતમ તરંગ લંબાઈ $0.25 × 10^{10}$ છે.
- 2$H-$ પરમાણુની આયનીકરણા ક્ષમતા $13.6 \;ev$ છે. જ્યારે $970.6\;\mathring A$ પ્રવેગિત કરવામાં આવે, તો બોહર મોડેલ અનુસાર ઉત્સર્જિત રેખાઓની સંખ્યા કેટલી થશે?View Solution
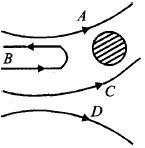
- 3રુથરફોર્ડના પ્રયોગમાં ન્યૂલિયસમાંથી નિકળતા $\alpha -$ કણોનું વિખેરણ નીચે દર્શાવેલ છે. તો નીચે પૈકી કયો પથ શકય નથી?View Solution
- 4View Solutionલિથિયમના દ્વિ આયોનિક પરમાણુની લાયમેન શ્રેણી પ્રથમ રેખાની તરંગલંબાઈ અને ડ્યુટેરીયમની લાયમેન શ્રેણીની પ્રથમ રેખાની તરંગલંબાઈ નો ગુણોત્તર શોધો.
- 5હાઈડ્રોજન પરમાણુમાં ધરાસ્થિતિમાં રહેલા ઈલેક્ટ્રોનની બંધનઊર્જા $13.6\,eV$ છે.$Li ^{2+}$માં દ્રિતીય ઉત્તેજીત અવસ્થામાં રહેલા ઈલેક્ટ્રોનને દૂર કરવા માટે જરૂરી ઊર્જા $c \times 10^{-1}\,eV$ છે.$x$નું $...........$ મૂલ્ય થશે.View Solution
- 6હાઇડ્રોજનની પ્રથમ ઉત્તેજિત અવસ્થામાં ઊર્જા $-3.4 \,eV$ છે. તેની ગતિઊર્જા ($eV$ માં) કેટલી થાય?View Solution
- 7બિન-સાપેક્ષતાવાદી અભિગમનો ઉપયોગ કરીને, $He^+ $ ની ત્રીજી કક્ષામાં રહેલ ઇલેકટ્રોનની ઝડપ કેટલી હશે? [આપેલ $K= 9 \times 10^9\; N\,m^2\,C^{-2}$ અચળાંક , $Z=2$ અને પ્લાન્ક અચળાંક $h= 6.6 \times 10^{-34 } \;Js$]View Solution
- 8હાઈડ્રોજન પરમાણુ ઉત્તેજીત અવસ્થામાંથી $\lambda$ તરંગલંબાઈ ધરાવતા ફોટોનનું ઉત્સર્જન કરીને ધરા સ્થિતિમાં આવે છે. ઉત્તેજીત અવસ્થા માટે મુખ્ય કવોન્ટમ નંબર '$n$' નું મૂલ્ય $.........$ થશે. ($R :$ રીડબર્ગ અચળાંક)View Solution
- 9ડ્યુટેરોન $(_1^2D)$ના વર્ણપટ્ટ સાથે સંકળાયેલ તરંગલંબાઈ હાઇડ્રોજનના વર્ણપટ્ટ સાથે સંકળાયેલ તરંગલંબાઈ કરતાં થોડીક અલગ હશે કારણ કે.....View Solution
- 10બોહરના મોડલમાં પ્રથમ કક્ષાની આણ્વિય ત્રિજ્યા ${r_0}$ હોય તો ચોથી કક્ષાની ત્રિજ્યા કેટલી હશે?View Solution