As both metal wires are of identical dimensions, so their length and area of cross-section will be same. Let them be \(l\) and \(A\) respectively. Then the resistance of the first wire is
\(R_{1}=\frac{l}{\sigma_{1} A}\) ...\((i)\)
and that of the second wire is
\(R_{2}=\frac{l}{\sigma_{2} A}\) ....\((ii)\)
As they are connected in series, so their effective
resistance is
\(R_{s} =R_{1}+R_{2} \)
\(=\frac{l}{\sigma_{1} A}+\frac{l}{\sigma_{2} A}\) \( \quad(\text { using }(\mathrm{i}) \text { and (ii) })\)
\(=\frac{l}{A}\left(\frac{1}{\sigma_{1}}+\frac{1}{\sigma_{2}}\right)\) ....\((iii)\)
If \(\sigma_{\mathrm{eff}}\) is the effective conductivity of the combination, then
\(R_{s}=\frac{2 l}{\sigma_{\mathrm{eff}} A}\) ....\((iv)\)
Equating eqns. \((iii)\) and \((iv),\) we get
\({\frac{2 l}{\sigma_{\mathrm{eff}} A}=\frac{l}{A}\left(\frac{1}{\sigma_{1}}+\frac{1}{\sigma_{2}}\right)} \)
\({\frac{2}{\sigma_{\mathrm{eff}}}=\frac{\sigma_{2}+\sigma_{1}}{\sigma_{1} \sigma_{2}} \text { or } \sigma_{\mathrm{eff}}=\frac{2 \sigma_{1} \sigma_{2}}{\sigma_{1}+\sigma_{2}}}\)
Download our appand get started for free
Similar Questions
- 1બે ગૂંચળાઓને જ્યારે સમાન ઉદ્દગમ સાથે જોડતાં સમાન ઉષ્મા ઉત્પન્ન કરવા માટે અનુક્રમે $20$ મીનીટ અને $60$ મીનીટ સમય લાગે છે. જે તેઓને સમાન ઉદ્દગમ સાથે સમાંતર ગોઠવણમાં જોડવામાં આવે તો સમાન પ્રમાણમાં ઉષ્મા ઉત્પન્ન કરવા માટ લાગતો સમય ........... મીનીટ હશે.View Solution
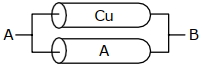
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે $25\, {cm}$ લંબાઈ અને $3\, {mm}^{2}$ આડછેદનું ક્ષેત્રફળ ધરાવતા કોપર$(Cu)$ ના સળિયાને બીજા સમાન એલ્યુમિનિયમ $(Al)$ ના સળિયા સાથે જોડેલ છે. $A$ અને $B$ બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ (${m} \Omega$ માં) શોધો.View Solution
(કોપરની અવરોધકતા $=1.7 \times 10^{-8}\, \Omega \,{m}$, એલ્યુમિનિયમની અવરોધકતા $=2.6 \times 10^{-8}\, \Omega \,{m}$ લો)
- 3$l$ લંબાઈ અને $A$ આડછેડનું ક્ષેત્રફળ અને $\rho $ ઘનતા ધરાવતા તારની વચ્ચે $V$ વૉલ્ટેજની બેટરી લગાવતા તેમાંથી પ્રવાહ પસાર થાય છે. જો સમાન દ્રવયના બનેલા બમણી લંબાઈ અને અડધા આડછેડનું ક્ષેત્રફળ વાળા તાર વચ્ચે આ બેટરી લગાવતા તેમાંથી કેટલો પ્રવાહ પસાર થાય?View Solution
- 4એક વિદ્યુતપરિપથમાં $100\,\Omega$ અને $200\,\Omega$ નો અવરોધ ધરાવતા બે અવરોધોને સમાંતરમાં જોડવામાં આવેલ છે. આપેલા સમયમાં $100 \Omega$ ના અવરોધમાં ઉત્પન્ન થતી ઉષ્મીય ઊર્જા અને તે $200 \Omega$ ના અવરોઘમાં ઉત્પન્ન થતી ઉષ્મીય ઊર્જાનો ગુણોત્તર હશે.View Solution
- 5તારમાંથી પસાર થતો પ્રવાહ $I = 2t + 3{t^2}$ હોય,તો $2\, sec$ થી $3\, sec$ ના ગાળામાં કેટલા .............. $C$ વિદ્યુતભાર પસાર થાય?View Solution
- 6$800\,^oC$ તાપમાને હીટરનો પાવર $500\,W$ છે. તો $200\,^oC$ તાપમાને પાવર કેટલા .............. $W$ હશે ? તેનો $\alpha$ = $4 \times 10^{-4}/\,^oC$.View Solution
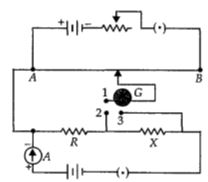
- 7આકૃતિમાં બતાવ્યા પ્રમાણે પોટેન્શિયોમીટરનો પરિપથ ગોઠવવામાં આવ્યો છે. પોટેન્શિયોમીટરના તાર પર વિદ્યુતસ્થિતિમાન પ્રચલન $K\, V/cm $ છે અને જ્યારે દ્રીમાર્ગી કળ બંધ હોય ત્યાંરે પરિપથમાં રહેલ એમિટર $1\,A $ દર્શાવે છે. જયારે કળ ટર્મિનલ $(i)\;1$ અને $2\;$ $(ii)\;1$ અને $ 3$ વચ્ચે જોડવામા આવે ત્યારે તટસ્થ લંબાઇ અનુક્રમે $l_1$ અને $l_2$ મળે છે. તો અવરોધ $R$ અને $X$ નું મૂલ્ય $ohm$ માં અનુક્રમે કેટલું હશે?View Solution
- 8View Solutionવિદ્યુતપ્રવાહ એ દિશા અને મુલ્ય બંને ધરાવે છે. તો તેને શું કહે છે.
- 9$50\,\Omega $ અને $100\,\Omega $ ના અવરોધને શ્રેણીમાં જોડીને $2.4\, V$ ની બેટરી સાથે જોડવામાં આવે છે.$100\, Ω $ ના વોલ્ટમીટરને $100\,Ω$ અવરોધ સાથે જોડતાં વોલ્ટમીટરનું અવલોકન કેટલા ........... $V$ થાય?View Solution
- 10View Solutionએક પ્રયોગમાં બેટરીના બે છેડા વચ્ચેના વિધુતસ્થીતિમાનના તફાવત વિરુદ્ધ પરીપથના પ્રવાહનો આલેખ દોરવામાં આવે છે. તો બેટરીનો આંતરીક વાહકત્વ .... હશે.