બે જુદા-જુદા તાપમાન $T_1$ અને $T_2$ એ એક બંધ પ્રણાલીમાં આદર્શ વાયુનું પ્રતિવર્તી સમતાપી વિસ્તરણ ધ્યાનમાં લો $(T_1 < T_2)$. અંતિમ કદ $(V)$ પર આધારિત થયેલા કાર્ય $(w)$ નું સચોટ આલેખીય વર્ણન નીચે પૈકી ક્યાં આલેખમાં છે?
- A
- B
- C
- D
JEE MAIN 2019, Diffcult
Download our app for free and get started
a
Let the gas is expanded from \(V_1\) to \(V\) at \(T_1\) and from \(V_2\) to \(V\) at \(T_2\)
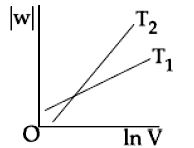
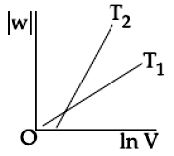
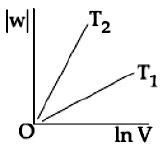
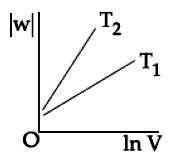
Let the gas is expanded from \(V_1\) to \(V\) at \(T_1\) and from \(V_2\) to \(V\) at \(T_2\)
\(\therefore \) At \(T_1\)
\([{W_1}] = nR{T_1}\,\ln \,\frac{V}{{{V_1}}} = nRT\,(\ln \,V - \ln \,{V_1})\)
\(Similarly\,at\,{T_2}\)
\([{W_2}] - nR{T_2}(\ln \,V - \ln \,{V_2})\)
\(\therefore \,{W_1} = nR{T_1}\ln \,V - nR{T_1}\,\ln \,{V_1}\)
\({W_2} = nR{T_2}\,\ln \,V - nR{T_2}\,\ln \,{V_2}\)
Slope of \({W_2} > \) Slope of \(W_1\)
As \(nR{T_2} > nR{T_1}({T_2} > {T_1})\)
\(\therefore \) The intercept of \(W_2\) is more negative than that of \(W_1\) because \(V_2 > V_1.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નિરપેક્ષ તાપમાન $T$ એ એક રાસાયણિક પ્રક્રિયા માટે પ્રમાણિત પ્રક્રિયા ગીબ્સ ઊર્જા નીચે મુજબ આપી શકાય,View Solution
${\Delta _r}{G^o} = A - BT$
જ્યાં $A$ અને $B$ શૂન્ય સિવાયના અચળાંકો છે. આ પ્રક્રિયા માટે નીચે આપેલા માંથી કયું સાચું છે?
- 2નીચેના પ્રકમો પરથી પ્રકિયા $B + D \rightarrow E + 2C$ માટે $\Delta H$ નું મૂલ્ય કેટલા ........... $\mathrm{kJ/mol}$ હશે તે જણાવો.View Solution
$\Delta H \,(kJ/mol)$ $\frac 12 A \rightarrow B$ $+150$ $3B \rightarrow 2C + D$ $-125$ $E + A \rightarrow 2D$ $+350$ - 3$(i)$ ટેકરીની ઊચાઈ $(ii)$ ટેકરીના ચડવામાં કપાતું અંતર $(iii)$ ટેકરીમાં ચડવાની ઊર્જા ફેરફાર માં કયું અવસ્થા વિધેય છે ?View Solution
- 4આપેલ આકૃતિના આધારે, સાયા વિધાન/નો ની સંખ્યા $.........$ છે.View Solution
$A.$ જથ્થામાં (બલ્કમાં) પ્રવાહી અણુ પર આકર્ષણ અને અપાકર્ષણ બળો સમાન રીતે વર્તે ત્યારે પૃષ્ઠતાણનું નિર્માણ થાય છે.
$B.$ સપાટી ઉપર હાજર અણુઓ પર અસમાન બળો પ્રવર્તમાન $(uneven\,forces)$ના કારણે પૃષ્ઠતાણ છે.
$C.$ જથ્થામાં (બલ્કમાં) અણુ પ્રવાહી સપાટી (સ્તર) પર આવતાં નથી.
$D.$ જો પ્રણાલી એ બંધ પ્રણાલી હોય તો સપાટી ઉપરના અણુઓ એ બાષ્પદબાણ માટે જવાબદાર છે.
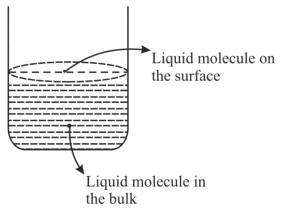
- 5પ્રક્રિયા માટે $ℓ\,n\, K_{eq}$ વિરૂદ્ધ તાપમાનનો આલેખ દોરવામાં આવે તો પ્રક્રિયા...... હોવી જોઈએ.View Solution
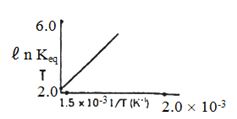
- 6આપેલ બંધઊર્જાના મૂલ્યો પરથી નીચેની પ્રક્રિયાની એન્થાલ્પી કેટલા ................ $\mathrm{kJ \,mol}^{-1}$ થશે ?View Solution
$H - H$ બંધઊર્જા $:\, 431.37 \,kJ\, mol^{-1}$ $C= C$ બંધઊર્જા $:\, 606.10\, kJ \,mol^{-1}$ $C - C$ બંધઊર્જા $:\, 336.49\, kJ\, mol^{-1}$ $C - H$ બંધઊર્જા $:\, 410.50\, kJ\, mol^{-1}$ પ્રક્રિયા : $\begin{array}{*{20}{c}}
{H\,\,\,\,H} \\
{|\,\,\,\,\,\,\,\,|} \\
{C = C} \\
{|\,\,\,\,\,\,\,\,\,|} \\
{H\,\,\,\,H}
\end{array}\, + \,H - H\, \to \,\begin{array}{*{20}{c}}
{H\,\,\,\,H} \\
{|\,\,\,\,\,\,\,\,|} \\
{H - C - C - H} \\
{|\,\,\,\,\,\,\,\,\,|} \\
{H\,\,\,\,H}
\end{array}\,$ - 7View Solutionમિથેનમાંથી મિથાઈલ રેડિકલની રચના કરતાં ટોલ્યુઇનમાંથી બેન્ઝાઈલ રેડિકલ બનાવવા માટે જરૂરી બંધ વિયોજન ઊર્જા એ ..... છે.
- 8પ્રબળ એસિડ અને પ્રબળ બેઈઝના તટસ્થીકરણથી પ્રતિ મોલ $H^+$ આયનોએ ઉદભવતી ઉષ્મા એ ...... હોય છે.View Solution
- 9$NCl_3$ જેવાં વિસ્ફોટક પદાર્થની $\Delta H_f^o$ નિર્માણ ઉષ્મા ...... થશે.View Solution
- 10નીચેના માંથી ક્યાં સંબંધો સાચાં છે?View Solution
$(A)$ $\Delta U = q + p \Delta V$
$(B)$ $\Delta G =\Delta H - T \Delta S$
$(C)$ $\Delta S =\frac{ q _{ rev }}{ T }$
$(D)$ $\Delta H =\Delta U -\Delta nRT$
નીચે આપેલા વિકલ્પોમાંથી યોગ્ય ઉત્તર પસંદ કરો.