બે લાંબા $8\,A$ અને $15\,A$ વીજ પ્રવાહ ધારિત સમાંતર તારને એકબીજાથી $7\,cm$ ના અંતરે રખેલ છે. બંને તારથી સમાન અંતરે બિંદુ $P$ એવી રીતે આવેલું છે કે જેથી બિંદુ $P$ ને તાર સાથે જોડતી રેખાઓ પરસ્પર લંબ થાય. તો $P$ બિંદુુએ ચુંબકીય ક્ષેત્રનું મૂલ્ય $............\times 10^{-6} T$ છે. $\left(\sqrt{2}=1.4\right)$ આપેલું છે.
JEE MAIN 2023, Diffcult
b
Magnetic fields due to both wires will be perpendicular to each other.
Magnetic fields due to both wires will be perpendicular to each other.
\(B _1=\frac{\mu_0 i _1}{2 \pi d } \quad B _2=\frac{\mu_0 i _2}{2 \pi d }\)
\(B _{\text {net }}=\sqrt{ B _1^2+ B _2^2} \Rightarrow \frac{\mu_0}{2 \pi d } \sqrt{ i _1^2+ i _2^2}\)
\(\Rightarrow \frac{4 \pi \times 10^{-7}}{2 \pi \times(7 / \sqrt{2}) \times 10^{-2}} \times \sqrt{8^2+15^2}\left( d =\frac{7}{\sqrt{2}}\,cm \right)\)
\(\Rightarrow 68 \times 10^{-6}\,T\)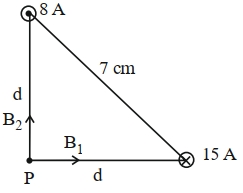
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$15 \,cm$ જેટલી સરેરાશ ત્રિજ્યાની રોલેન્ડ $(Rowland)$ રીંગના, $800$ જેટલી સાપેક્ષ પરમિએબિલીટી ધરાવતા કોર પર તારના $3500$ આંટા વિંટાળવામાં આવેલ છે. $1.2\, A$ જેટલા મેગ્નેટાઇઝીંગ વિદ્યુતપ્રવાહ માટે કોરમાં ચુંબકીય ક્ષેત્ર $B$ કેટલું હશે?View Solution
- 2$(i)$ પ્રવાહધારિત કોઇલની ચુંબકીય મોમેન્ટ એ ત્રિજ્યાના ક્યા પ્રમાણમાં છે?View Solution
- 3$5\,Ω$ અવરોધ ધરાવતુ એમિટર $5\, mA$ માપી શકે છે.હવે તેને $100\,V$ માપે તેવું બનાવવા માટે કેટલા ............ $\Omega $ અવરોધ શ્રેણીમાં જોડવો પડે?View Solution
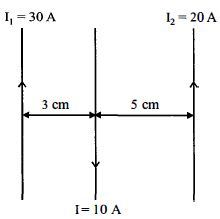
- 4ત્રણ સમાંતર વાહકોમાંથી આકૃતિમાં દર્શાવ્યા પ્રમાણે પ્રવાહ વહે છે. વચ્ચે રહેલ $25\,cm$ લંબાઈના વાહક દ્વારા કેટલું બળ અનુભવાતું હશે?View Solution
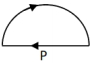
- 5$r$ ત્રિજ્યાનું અર્ધવર્તુળ અને વ્યાસ પરના તારમાં સમાન પ્રવાહ $i$ વહે છે, તો કેન્દ્ર પર રહેલા $P$ ખંડ પર એકમ લંબાઈ દીઠ લાગતું ચુંબકીય બળ કેટલું હશે?View Solution
- 6એક પ્રયોગમાં, સ્થિર સ્થિતિમાંથી ઈલેક્ટ્રૉનને $500 \,V$ લાગુ પાડીને પ્રવેગિત કરવામાં આવે છે. હવે જો $100\, mT$ જેટલું ચુંબકીય ક્ષેત્ર લાગુ પાડવામાં આવે તો ગતિ પથની ત્રિજ્યા કેટલી થશે? (ઇલેકટ્રોન પરનો વિદ્યુતભાર $=1.6 \times 10^{-19}\, C,$ ઇલેક્ટ્રૉનનું દળ $=9.1 \times 10^{-31}\, kg)$View Solution
- 7$25\,\Omega $ અવરોધ ધરાવતા ગેલ્વેનોમીટરના પૂર્ણ આવર્તન માટે $1\,mA$ પ્રવાહની જરૂર પડે છે. $2\,A$ પ્રવાહનું આવર્તન દર્શાવે તેવો એમીટર બનાવવા માટે તેની સાથે કેટલા મૂલ્યનો શંટ અવરોધ જોડાવો પડે?View Solution
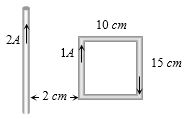
- 8View Solutionઆપેલ આકૃતિ માં રહેલ લૂપ પર કેટલું બળ લાગતું હશે?
- 9View Solutionજો સ્પિંગમાંથી વિદ્યુતપ્રવાહ પસાર કરવામાં આવે, તો તે
- 10$0.049 \mathrm{~T}$ જેટલા સમાન ચુંબકીય ક્ષેત્રમાં, એક ચુંબકીય સોય આકૃતિમાં દર્શાવ્યા પ્રમાણે $5$ સેકન્ડમાં $20$ પૂર્ણ દોલનો કરે છે. સોયની જડત્વની ચાકમાત્રા $9.8 \times 10^{-6} \mathrm{~kg} \mathrm{~m}^2$છે. જો સોયની સુંબકીય ચાકમાત્રા $x \times 10^{-5} \mathrm{Am}^2$ હોય તો ' $x$ ' નું મૂલ્ય. . . . . . . .થશે.View Solution
