બે $m$ દળના બ્લોક $A $ અને $B$ ને $L$ લંબાઇ અને $k$ બળઅચળાંક ધરાવતી સ્પિંગ્ર વડે જોડેલાં છે. $m$ દળ ધરાવતો $C$ બ્લોક $v$ વેગથી ગતિ કરીને $A$ સાથે અથડાતા સ્પિંગ્રનું મહત્તમ સંકોચન કેટલું થાય?
Diffcult
a
(a)Initial momentum of the system (block \(C\)) \(= mv\)
After striking with \(A\), the block \(C\) comes to rest and now both block \(A\) and \(B\) moves with velocity \(V\), when compression in spring is maximum.
By the law of conservation of linear momentum
\(mv = (m + m) V\) ==> \(V = \frac{v}{2}\)
By the law of conservation of energy
\(K.E.\) of block \(C = K.E. \) of system \(+ P.E.\) of system
\(\frac{1}{2}m{v^2} = \frac{1}{2}(2m)\,{V^2} + \frac{1}{2}k{x^2}\)
==> \(\frac{1}{2}m{v^2} = \frac{1}{2}(2m)\;{\left( {\frac{v}{2}} \right)^2} + \frac{1}{2}k{x^2}\)
==> \(k{x^2} = \frac{1}{2}m{v^2}\)
==> \(x = v\sqrt {\frac{m}{{2k}}} \)
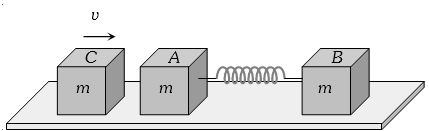
(a)Initial momentum of the system (block \(C\)) \(= mv\)
After striking with \(A\), the block \(C\) comes to rest and now both block \(A\) and \(B\) moves with velocity \(V\), when compression in spring is maximum.
By the law of conservation of linear momentum
\(mv = (m + m) V\) ==> \(V = \frac{v}{2}\)
By the law of conservation of energy
\(K.E.\) of block \(C = K.E. \) of system \(+ P.E.\) of system
\(\frac{1}{2}m{v^2} = \frac{1}{2}(2m)\,{V^2} + \frac{1}{2}k{x^2}\)
==> \(\frac{1}{2}m{v^2} = \frac{1}{2}(2m)\;{\left( {\frac{v}{2}} \right)^2} + \frac{1}{2}k{x^2}\)
==> \(k{x^2} = \frac{1}{2}m{v^2}\)
==> \(x = v\sqrt {\frac{m}{{2k}}} \)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પદાર્થ $ 'A' $ સુરેખ રેખા પર $v $ વેગથી ગતિ કરીને સ્થિર રહેલાં પદાર્થ $'B'$ સાથે સંઘાત અનુભવે છે. સંઘાત બાદ $B \;\;1.6v $ જેટલો વેગ પ્રાપ્ત કરે છે. ધારો કે પદાર્થ સંપૂર્ણ પણે સ્થિર સ્થાપક છે, તો $A$ ના કેટલા .............. ટકા ઊર્જા સંઘાત દ્વારા $B$ સાથે વિનિમય પામશે ?View Solution
- 2$5\; kg$ દળના પદાર્થનું વેગમાન $10\; kg-m/s$ છે.તેના પર $0.2\; N $ બળ $ 10 \;seconds $ સમય સુધી લાગતાં ગતિઊર્જામાં થતો વધારો.....$J$View Solution
- 3કોઈ વ્યક્તિનું હદય, ધમનીમાં $150\;mm$ જેટલા પારાના દબાણે $5$ લિટર લોહીનું પ્રતિ મિનિટે પમ્પિગ કરે છે. જો પારાની ઘનતા $13.6 \times 10^3\; kg/m^3$ અને $ g=10 \;m/s^2 $ હોય, તો હદયનો પાવર (વોટમાં) કેટલો હશે?View Solution
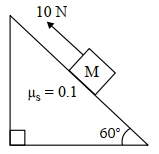
- 4$1$ kg દળ ધરાવતા ચોસલાને સમક્ષિતિજથી $60^{\circ}$ના કોણે રહેલી ઢળતી સપાટી ઉપરઆકૃતિમાં દર્શાવ્યા અનુસાર ઢળતી સપાટીને સમાંતર એવા $10 \mathrm{~N}$ ના બળ વડે ઉપર તરફ ધક્કો મારવામાં આવે છે. આફૃતિમાં દર્શાવ્યા અનુસાર જો ચોસલું ઢળતી સપાટીને સમાંતર $10 \mathrm{~m}$ ઉપર ધકેલાય આવે તો ધર્ષણબળની વિરુદ્ધ થતું કાર્ય__________થશે.View Solution
$\text { [ } g=10 \mathrm{~m} / \mathrm{s}^2]$લો.
- 5કણ $A$ એ સ્થિર સ્થિતિમાં રહેલા બીજા કણ $B$ સાથે સંપૂર્ણ સ્થિતિસ્થાપક અથડામણ પામે છે. તેઓ એકબીજાથી વિરુદ્ધ દિશામાં સરખી ઝડપથી ઉડે છે. જો તેમના દળ અનુક્રમે $m_A$ અને $m_B$ હોય તોView Solution
- 6$200\,g$ નો એક બોલ $20\,m$ ઊંચા થાંભલા ઉપર સ્થિર સ્થિતિમાં છે.$10\,g$ ની અને $u\,m/s$ ના વેગથી સમક્ષિતિજ દિશામાં ગતિ કરતી એક ગોળી (બુલેટ) બોલના કેન્દ્રને અથડાય છે સંઘાત બાદ બંને એકબીજાથી સ્વતંત્ર રીતે ગતિ કરે છે.બોલ જમીન ઉપર થાંભલાના તળિયે થી $30\,m$ અંતરે અને બુલેટ $120\,m$ અંતરે પડે છે. બુલેટનો વેગ $..............m/s$ હશે.($\left.g =10 m / s ^2\right.$ છે.)View Solution
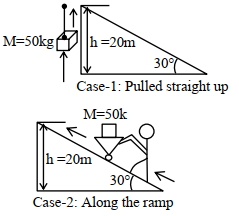
- 7$50 \mathrm{~kg}$ ની વસ્તુને જમીનથી $20 \mathrm{~m}$ ઉંચાઈ સુધી આકૃતિમાં દર્રાવ્યા મુજબ બે જુદી-જુદી રીતે ઉંચકવામાં આવે છે. બંને કિસ્સામાં અનુક્રમે ગુરુત્વાકર્ષણ બળની વિરુધ્ધ કરવું પડતું કાર્ય નો ગુણોત્તર . . . . .થશેView Solution
- 8$200gm$ અને $ 400 gm $ દળ ધરાવતા રબરના બે દડા $ A$ અને $ B$ વિરુધ્ધ દિશામાં ગતિ કરે છે.$A$ દડાનો વેગ $0.3 m/s $ છે,અથડામણ પછી બંને દડા સ્થિર થઇ જતાં હોય,તો $ B $ દડાનો વેગ કેટલા ................ $\mathrm{m} / \mathrm{s} $ થશે?View Solution
- 9$m$ દળનો એક પદાર્થ $v$ વેગથી પ્રારંભમાં સ્થિર સ્થિતિમાં રહેલો $2m$ દળના બીજા પદાર્થ સાથે હેડઓન સંઘાત કરે છે. સંઘાત પહેલા અને સંઘાત પછી સંઘાતી પદાર્થની ગતિ ઊર્જાનો ગુણોત્તર શું હશે ?View Solution
- 10$0.25 Hp$ ની મોટર $600 rpm$ ની ઝડપથી ભ્રમણ કરે છે.જો કાર્યક્ષમતા $40\%$ હોય,તો એક પરિભ્રમણ પૂર્ણ કરતાં કેટલું કાર્ય થશે?View Solution
