$ (B{e^{ + + + }}) $ ની કેટલામી કક્ષાની ત્રિજયા હાઇડ્રોજનની ધરા-સ્થિતિની ત્રિજયા જેટલી થાય?
Medium
Download our app for free and get started
c
(c) Radius of \(n^{th}\) orbit for any hydrogen like atom
(c) Radius of \(n^{th}\) orbit for any hydrogen like atom
\({r_n} = {r_0}\left( {\frac{{{n^2}}}{Z}} \right)\) (\({r_0} = \) radius of first orbit of \({H_2}\)-atom)
If \({r_n} = {r_0}\) ==> \(n = \sqrt Z .\) For \(Be+++, Z = 4\) ==>\(n = 2.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$X-ray$ ની તરંગલંબાઈ $0.010 \ Å$ હોય તો તેનું વેગમાન કેટલું થાય?View Solution
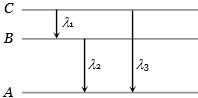
- 2ચોક્કસ અણુના $A, B, C$ ઉર્જા સ્તરો માટે વધતી ઊર્જાના મૂલ્યો ${E_A} < {E_B} < {E_C}$ છે. જો ${\lambda _1},\;{\lambda _2},\;{\lambda _3}$ અનુક્રમે $C$ થી $B, \;B$ થી $A$ અને $C$ થી $A$ સંક્રાતિ દરમિયાન ઉત્સર્જન થતી તરંગલંબાઇ હોય, તો કયું વિધાન સાચું થાય?View Solution
- 3હાઈડ્રોજન પરમાણુની પ્રથમ કક્ષાની ત્રિજ્યા $ 0.5 \,Å $ અને ઈલેક્ટ્રોનની ઝડપ $2.2 ×10^6\, m /sec$ છે. તો ઈલેક્ટ્રોન ની ગતિના લીધે પ્રોટોન પાસે ઉદ્દભવતું ચુંબકીય પ્રેરણ......$Tesla$ શોધો.View Solution
- 4નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ : હાઈડ્રોજન પરમાણુમાં જ્યારે ઈલેકટ્રોન નીચી ઊર્જા કક્ષા $\left( E _{1}\right)$ માંથી ઉચ્ચ ઊર્જા કક્ષા $\left(E_{2}\right)$ માં કૂદકો (સંક્રાંત) કરે છે ત્યારે ઉત્સર્જાતા વિકિરણની આવૃત્તિ $h f= E _{1}- E _{2}$ વડે આપી શકાય છે.
વિધાન $II$ : ઉચ્ય ઊર્જા કક્ષામાંથી નીચી ઊર્જ કક્ષામાં ઈલેકટ્રોનની સંક્રાંતિ, વિકિરણ આવૃત્તિ $f=\left( E _{2}- E _{1}\right) / h$ સાથે સંકળાયેલ છે.
આ શરતને બોહરની આવૃત્તિ શરત કહે છે.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 5હાઇડ્રોજન પરમાણુમાં $n = 2$ અને $n = 3$ કક્ષામાં રહેલી ઊર્જાનો તફાવત $E$ હોય, તો ધરા-સ્થિતિમાં રહેલા ઇલેકટ્રોનને દૂર કરવા માટે કેટલા ........$E$ ઉર્જાની જરૂર પડે?View Solution
- 6ઊર્જાનો એકમ રીડબર્ગ બરાબર અચળાંક ......$eV$ છે.View Solution
- 7View Solutionઆપેલ પ્રવેગિત વોલ્ટેજ આગળ ક્ષ કિરણો ટ્યૂબમાં ક્ષ કિરણો ઉત્પન્ન થાય છે. સતત ક્ષ કિરણોની તરંગ લંબાઈનું મૂલ્ય .......હશે.
- 8View Solutionહાઇડ્રોજનમાં કઇ સંક્રાતિમાં સૌથી વધુ આવૃત્તિવાળો ફોટોન ઉત્સર્જન થાય?
- 9$ {90^o} $ ના ખૂણે પ્રકીર્ણન પામતા કણો $56$ હોય,તો $ {60^o} $ ના ખૂણે પ્રકીર્ણન પામતા કણો કેટલા હોય?View Solution
- 10View Solutionવર્ણપટરેખાઓની પાશ્ચન શ્રેણીમાં ટૂંકામાં ટૂંકી કઈ તરંગલંબાઈ હાજર છે?