Let \(µ_s\) and \(µ_k\) be the coefficients of static and kinetic friction between the box and the plank respectively.
When the angle of inclination \(0\) reaches \(30°\), the block just slides, \(\mu_s=\tan\theta =\tan 30^o = \frac{1}{\sqrt3}=0.6\)
If \(a\) is the acceleration produced in the block, then
\(ma = mg\sin\theta -f_k\)
(where \(f_k \) is force of kinetic friction)
\(= mg\sin0 -μ_k N\) \((as\ \ f_k. = μ_k N)\)
\(= mg\sin0 - μ_kmg\cos\theta\) \((as\ \ N = mgcos\theta)\)
\(a = g(\sin\theta - μ_k\cos\theta)\)
As \( g = 10 ms^{- 2}\) and \(0 = 30°\)
\(a = ( 10 ms^{- 2})(sin30^o -μ_kcos30^o)\) ..........\((i)\)
If \(s\) is the distance travelled by the block in time \(t\), then
\(S=\frac{1}{2} at^2\) \((u=0)\)
\(a=\frac{2s}{t^2}\)
But \(s=4.0 \ m\) and \(t=4.0 \ s\) (given)
\(a=\frac{2(4.0\ m)}{(4.0\ s)^2}=\frac{1}{2}\ ms^{-2}\)
Substituting this value of \(a\) in eqn. \((i)\), we get
\(\frac{1}{2}\ ms^{-2} =10\ ms^{-2}\left( \frac{1}{2}-\mu_k \frac{\sqrt3}{2} \right)\)
\(\frac{1}{10}=1-\sqrt3 \mu_k\) or \(\sqrt3 \mu_k=1-\frac{1}{10}=\frac{9}{10}=0.9\)
\(\mu_k =\frac{0.9}{\sqrt3}=0.5\)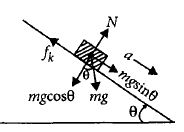
Download our appand get started for free
Similar Questions
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે, બળ $F_1$ ને એક બ્લોક પર લગાડવામાં આવે છે તો પણ બ્લોક ગતિ કરતો નથી. ત્યારબાદ શિરોલંબ દિશામાનાં બળ $F_2$ ને શૂન્યથી વધારવામાં આવે છે તો બ્લોક ગતિ કરવાનું શરુ કરે છે તો; સાયું નિવેદન ક્યું છેView Solution
- 2$m$ દળનાં બ્લોકને કેન્દ્રથી $x$ અંતરે સમક્ષિતિજ રીતે વર્તુળાકાર ટેબલ પર મુકવામાં આવેલો છે. જો બ્લોક અને ફરતાં ટેબલની સપાટી વચ્ચેનું ઘર્ષણાંક $\mu$ છે, તો ટેબલની મહત્તમ કોણીય ઝડપ શોધો કે જેથી બ્લોક તેના પરથી લપસે નહિ.View Solution
- 3બરફના બ્લોકને $\theta=45^°$ ઢાળવાળા રફ ઢાળ પરથી નીચે આવતા લાગતો સમય એ સમાન ઘર્ષણરહિત ઢાળ પરથી નીચે આવતા લાગતા સમય કરતાં બમણો હોય તો બ્લોક અને ઢાળ વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
- 4$5\, kg$ દળ ધરાવતા પદાર્થ સ્થિર સ્થિતિમાં છે જો તેના પર $24\, N$ બળ લાગવામાં આવે તો પદાર્થ ........ $m/s^2$ પ્રવેગ પ્રાપ્ત કરશે. ($\mu_k =0.4$)View Solution
- 5સમક્ષિતિજ સપાટી પર રહેલા એક ટ્રક ($\,\mu = 0.6$) પર $1\, kg$ નો બ્લોક પડેલો છે અને ટ્રકનો પ્રવેગ $ 5\,m/sec^2$ હોય, તો બ્લોક પર કેટલું ઘર્ષણ બળ ($N$ માં) લાગતું હશે?View Solution
- 6$5 \mathrm{~kg}$ દળના એક બ્લોકને આકૃતિમાં દર્શાવેલ ખરબચડા સમતલ પર મુકેલ છે. જો આ બ્લોકને ઉપર તરફ્ ખસેડવા લઘુતમ બળ $\vec{F}_1$ અને નીચે તરફ સરક્તો અટકાવવા જરૂરી બળ $\vec{F}_2$ હોય તો $\left|\vec{F}_1\right|-\left|\vec{F}_2\right|=\ldots \ldots \ldots . . \quad\left(g=10 \mathrm{~m} / \mathrm{s}^2\right.$ લેવુ.)View Solution
- 7જો કોઈ બ્લોક $5 \,m / s$.ના વેગ સાથે $30^{\circ}$ ઢોળાવવાળી સપાટી ૫ર ઊધ્વદિશામાં ગતિ કરે છે, તે $0.5 \,s$ પછી અટકી જાય છે, તો પછી ઘર્ષણાંક લગભગ કેટલું હશે ?View Solution
- 8View Solutionઆકૃતિમાં દર્શાવ્યા મુજબ એક ટ્રક અચળ ઝડપે ગતિ કરી રહ્યું છે. વાહનનું પરિણામી (કુલ) વજન છે
- 9$72 \,km/hr$ ની ઝડપથી જતી બાઇક $ 20\,m$ ત્રિજયામાં વળાંક લે છે,બાઇક સ્લીપ ન થાય તે માટે શિરોલંબ સાથે કેટલાના ખૂણે રાખવી જોઇએ?View Solution
- 10View Solutionમર્યાદિત ઘર્ષણ એ
