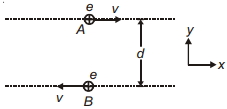
બે પ્રોટોન $A$ અને $B, x$-અક્ષને સમાંતર, પરસ્પર વિરુદ્ધ દિશામાં, સમાન ઝડપે $V$ સાથે ગતિ કરે છે. દર્શાવેલ ક્ષણે, પ્રોટોન $A$ પર લાગતા ચુંબકીય બળ અને વિદ્યુતબળનો ગુણોત્તર કેટલો છે ? ($c =$ શૂન્યાવકાશમાં પ્રકાશની ઝડ૫)

Medium
b
(b)
(b)
Magnetic field at \(A\) due to \(B\)
\(B=\frac{e v \sin 90^{\circ}}{d^2} \times \frac{\mu_0}{4 \pi}\)
\(B=\frac{e v}{d^2} \times \frac{\mu_0}{4 \pi}-(i)\)
Magnetic force on \(A\) is
\(F_B=e v B\)
From \((i)\), \(F_B=e v \frac{(e v)}{d^2} \times \frac{\mu_0}{4 \pi}\)
\(F_e=e t\)
\(=\frac{e Ke }{ d ^2}\)
\(\frac{F_B}{F_e}=\frac{e^2 v^2}{d^2} \times \frac{d^2}{e^2 k} \times \frac{\mu_0}{4 \pi}\)
\(=\frac{v^2}{\frac{1}{4 \pi \varepsilon_0} \times 4 \pi}\)
\(=\frac{v^2}{\frac{1}{\mu_0} \varepsilon_0}\)
\(\frac{F_B}{F_e}=\frac{v^2}{c^2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક લાંબા તારમાંથી સ્થાયી વિદ્યુતપ્રવાહ વહે છે. તેને એક આંટાવાળા વર્તુળમાં વાળતા બનતાં લૂપનાં કેન્દ્ર પર મળતું ચુંબકીયક્ષેત્ર $B$ છે. હવે તેને $n$ આંટાવાળા વર્તુળાકાર લૂપમાં વાળવામાં આવે છે. ગૂચળાંનાં કેન્દ્ર પર મળતું ચુંબકીય ક્ષેત્ર કેટલું હશે?View Solution
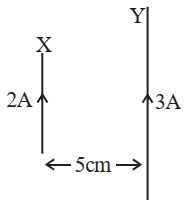
- 2$50\,cm$ લંબાઈના એક તાર $X$ને અને $2\; A$ પ્રવાહ ધરાવતા $5\,m$ લાંબા તાર $Y$ ને સમાંતર મૂકવામાં આવેલ છે. તાર માં $3\; A$ પ્રવાહ વહે છે. બે તારો વચ્ચેનું અંતર $5\,cm$ અને તેમાં સમાન દિશામાં પ્રવાહ વહે છે. $Y$ તાર ઉપર લાગતું બળ $..........$ હશે.View Solution
- 3$Z$ અક્ષ પર મૂકેલા તારમાંથી ૠણ $Z$ - દિશામાં $I$ પ્રવાહ પસાર થાય છે.તો બિંદુ $(x, y)$ આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 4એક ગેલ્વેનોમીટરનો અવરોધ $50 \Omega$ છે અને તે મહતમ $5 \mathrm{~mA}$ પ્રવાહને પસાર થવા દે છે.તેનું $100 \mathrm{~V}$ માપી શકે તેવા વોલ્ટ મીટરમાં રુંપાંતર કરવા માટે જોડવો પડતો જરૂરી શ્રેણી અવરોધ______$\Omega$છે.View Solution
- 5વેગ $\overrightarrow{\mathrm{u}}=3 \hat{\mathrm{i}}+5 \hat{\mathrm{j}} \mathrm{m} / \mathrm{s}$ અને ઈલેકટ્રોન પર લાગતું બળ $\vec{F}=5 \mathrm{ekN}$ છે. જ્યા e ઈલેકટ્રોન પરનો વિદ્યુતભાર છે. તો $B0$ નું મૂલ્ય .......... $T$View Solution
- 6$X-Z$ સમતલમાં ઉગમબિંદુ પર એક એક લંબચોરસ ($5\,cm\times 2\,cm$) $100\,$ આંટાવાળા ગુચળામાથી $3\,A$ પ્રવાહ સમઘડી દિશામાં વહે છે.$X$ અક્ષની દિશામાં $1\,T$ ચુંબકીય ક્ષેત્ર પ્રવર્તે છે.જો ગૂચળાંને $Z$ અક્ષ સાથે $45^o$ના ખૂણે વાળવામાં આવે તો તેના પર કેટલા ......$Nm$ ટોર્ક લાગે?View Solution
- 7$100$ આંટા, $5 \times 10^{-3} \mathrm{~m}^2$ નું ક્ષેત્રફળ અને $1 \mathrm{~mA}$ પ્રવાહ ધરાવતા એક ગૂંચળાને $0.20 \mathrm{~T}$ ના નિયમિત ચુંબકીય ક્ષેત્ર માં એવી રીતે મૂકવામાં આવે છે કે જેથી ગૂંચળાનું સમતલ ચુંબકીય ક્ષેત્રને લંબરૂપે રહે.. ગૂંચળાને $90^{\circ}$ ના કોણે ભ્રમણ કરાવવા માટે કરવું પડતું કાર્ય . . . . .$\mu \mathrm{J}$ થશે.View Solution
- 8View Solutionઅનિયમિત આકારની લૂપમાં પ્રવાહ પસાર કરીને ચુંબકીય ક્ષેત્રમાં મૂકવાથી ..... .
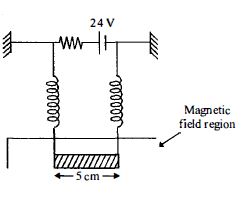
- 9આકૃતિમાં દર્શાવેલ પરિપથમાં ઉપર અને નીચે તાર અને જમણી અને ડાબી બાજુએ સમાન સ્પ્રિંગ છે. નીચેના તારનું દળ $10\, g$ અને લંબાઈ $5\, cm$ છે. તારના વજનને કારણે સ્પ્રિંગ $0.5\, cm$ જેટલી ખેંચાઇ છે. અને પરિપથનો કુલ અવરોધ $12\, \Omega $ છે. જ્યારે નીચેના તાર પર અચળ ચુંબકીય ક્ષેત્ર લગાવવામાં આવે ત્યારે સ્પ્રિંગ $0.3\, cm$જેટલી વધારે ખેંચાઇ છે. તો લગાવેલ ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
- 10View Solutionસમાન વેગ ધરાવતો એક પ્રોટોન અને આલ્ફા કણ નિયમિત ચુંબકીય ક્ષેત્ર કે જે ગતિને લંબરૂપ પ્રવર્તે છે, માં દાખલ થાય છે. આલ્ફા અને પ્રોટોન કણ દ્વારા અનુસરેલ વર્તુળાકાળ પથોની ત્રિજ્યાઓનો ગુણોત્તર ........... થશે.
