બે પથ્થરોને જમીન પરથી સમાન ઝડ૫ $u$ સાથે ઉપરની તરફ અલગ અલગ ખૂણો ઉછાળવામાં આવે છે. જેથી બંનેની સમક્ષિતિજ અવધિ સમાન હોય, જો પથ્થરો દ્વારા મેળવેલ ઊચાઈ $h_1$ અને $h_2$ હોય તો $h_1+h_2$ શું હશે?
Medium
b
(b)
(b)
If range is same then, one angle is \(\theta\) and other angle is \((90-\theta)\)
\(\Rightarrow h_1=\frac{u^2 \sin ^2 \theta}{2 g}, h_2=\frac{u^2 \sin ^2(90-\theta)}{2 g}\)
\(h_1=\frac{u^2 \sin ^2 \theta}{2 g}, h_2=\frac{u^2 \cos ^2 \theta}{2 g}\)
So, \(h_1+h_2 \Rightarrow \frac{u^2 \sin ^2 \theta}{2 g}+\frac{u^2 \cos ^2 \theta}{2 g}=\frac{u^2}{2 g}\left(\sin ^2 \theta+\cos ^2 \theta\right)\)
\(h_1+h_2=\frac{u^2}{2 g}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક તરવૈયાની સ્થિર પાણીમાં તરવાની ઝડપ $4\,km\,h ^{-1}$ છે. જો તરવૈયો $1\,km$ પહોળી નદીના વહનને લંબરૂપે $strokes$ (હાથની ગતિ) કરતો હોય તો તે સામેના કાંઠ લંબપાદથી $750\,m$ દૂર પહોંચે છે. નદીના પાણીની ઝડપ $...........\,km h ^{-1}$ હશે.View Solution
- 2$M$ દળના પદાર્થને $v$ વેગથી $\theta $ ખૂણે પ્રક્ષિપ્ત કરવામાં આવે છે,તો $t$ સમય પછી પદાર્થનો વેગ કેટલો થાય?View Solution
- 3View Solutionઘડિયાળમાં મિનિટ કાંટો અને કલાક કાંટાનો કોણીય ઝડપનો ગુણોત્તર કેટલો થાય?
- 4પ્રક્ષિપ્ત પદાર્થનો મહત્તમ ઊંચાઇએ વેગ શરૂઆતના વેગ કરતાં $\frac{1}{{\sqrt 2 }}$ ગણો હોય તો તેની અવધિ કેટલી થાય?View Solution
- 5ખભા ઉપર વાંદરો બેસાડીને એક વ્યક્તિ $9 \mathrm{~m}$ ત્રિજ્યા ઘરાવતા લીસા વત્તુળાકાર રસ્તા ઉપર સાઈકલ ચલાવે છે અને $3$ મીનીટમાં $120$ પરિભ્રમણો પૂર્ણ કરે છે. વાંદરા માટેના કેન્દ્રગામી પ્રવેગનું મૂલ્ય . . . . . હશે. ( $\mathrm{m} / \mathrm{s}^2$ માં) હશે.View Solution
- 6એક કણ ને $u$ વેગથી સમક્ષિતીજ સાથે $\alpha $ ખૂણે ફેકવામા આવે અને બીજા કણ ને તે જ વેગથી જ શિરોલંબ સાથે $\alpha$ ખૂણે ફેકવામા આવે તો તેમના ઉડ્ડયન સમયનો ગુણોત્તર કેટલો થાય?View Solution
- 7$m$ દળનો એક કણ $t = 0$ સમયે સ્થિર સ્થિતિમાં છે. તેને $x$ $-$ દિશામાં $F(t) = F_0e^{-bt}$ બળ લાગુ પાડવામાં આવે છે. નીચેનામાંથી કયા દ્વારા તેની ઝડપ $v(t)$ દર્શાવાય છે?View Solution
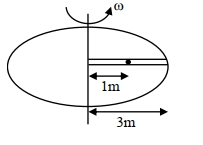
- 8એક વર્તુળાકા ટેબલ $\omega$ રેડિયન/સેકંડના કોણીય વેગથી તેની અક્ષને ફરતે ભ્રમણ કરે છે. ટેબલની ત્રિજ્યાવર્તી દિશામાં એક લીસો ખાંચો રહેલો છે. એક સ્ટીલના ગોળાને $1 \mathrm{~m}$ ના અંતરે ખાંચામાં હળવેકથી મૂકવામાં આવે છે. જો ટેબલની ત્રિજ્યા $3 \mathrm{~m}$ હોય, તો ગોળાનો ટેબલની સાપેક્ષ જે સમયે ગોળો ટેબલમાંથી છૂટે તેની સાપેક્ષ ત્રિજ્યાવર્તી વેગ $x \sqrt{2} \omega \mathrm{m} / \mathrm{s}$ છે, જ્યાં $x$ નું મૂલ્ય. . . . . . છે.View Solution
- 9એક દોલકને પ્રારંભિક $\omega$ $rpm$ જેટલી ઝડપ સાથે સમક્ષિતિજ સમતલમાં દોરી વરે ભ્રમણ કરાવવામાં આવે છે. દોરીમાં $T$ જેટલો તણાવ છે. ત્રિજ્યા સમાન રાખીને જો ઝડપ $2 \omega$ કરવામાં આવે તો દોરીમાં તણાવ. . . . . થશે.View Solution
- 10ચોક્કસ ગ્રહ (કોઈ વાતાવરણ વિના) પર જમીન પરથી ઉદ્ભવેલ પ્રક્ષેપણની સ્થાનનું નિર્દેશન $y=\left(4 t-2 t^2\right) m$ અને $x=(3 t) m$ દ્વારા આપવામાં આવે છે, જ્યાં $t$ સેકન્ડમાં છે અને પ્રક્ષેપણના બિંદુને ઉગમબિંદુ તરીકે લેવામાં આવે છે. શિરોલંબ સાથે પ્રક્ષિપ પદાર્થનો પ્રક્ષેપણ ખૂણો કેટલો હોય?View Solution
